Giúp mk câu 3 phần trắc nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)

A.Trắc nghiệm
Câu 1.A
Câu 2.D
Câu 3.A
Câu 4.C
Câu 5.D
Câu 6. A
B.Tự luận
Câu 10
a) Tia Ot nằm giữa hai tia còn lại vì góc xOt<góc xOy(40<80)
b) VÌ Tia Ot nằm giữa hai tia còn lại nên:
xOt+yOt=xOy
Thay xOt=40;xOy=80,ta có:
40+yOt=80
yOt=80-40
yOt=40
Vậy góc yOt = 40 độ
c)Tia Ot là tia phân giác của góc xOy vì:
+Tia Ot nằm giữa hai tia còn lại
+Góc xOt=góc yOt(40=40)

Refer
Có nhiều dạng năng lượng : cơ năng, nhiệt năng, điện năng, hóa năng, quang năng, năng lượng hạt nhân, động năng, thế năng, năng lượng bức xạ, ...............
Tuy nhiên đối với chương trình học lớp 9 thì bạn chỉ học 5 dạng:
+Cơ năng
+Nhiệt năng
+Điện năng
+Quang năng
+Hóa Năng
Vd: Trong một vụ sét đánh điển hình, 500 megajoules năng lượng điện năng được chuyển đổi thành cùng một năng lượng ở các dạng khác, chủ yếu là năng lượng ánh sáng, năng lượng âm thanh và năng lượng nhiệt.
 Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha
Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha




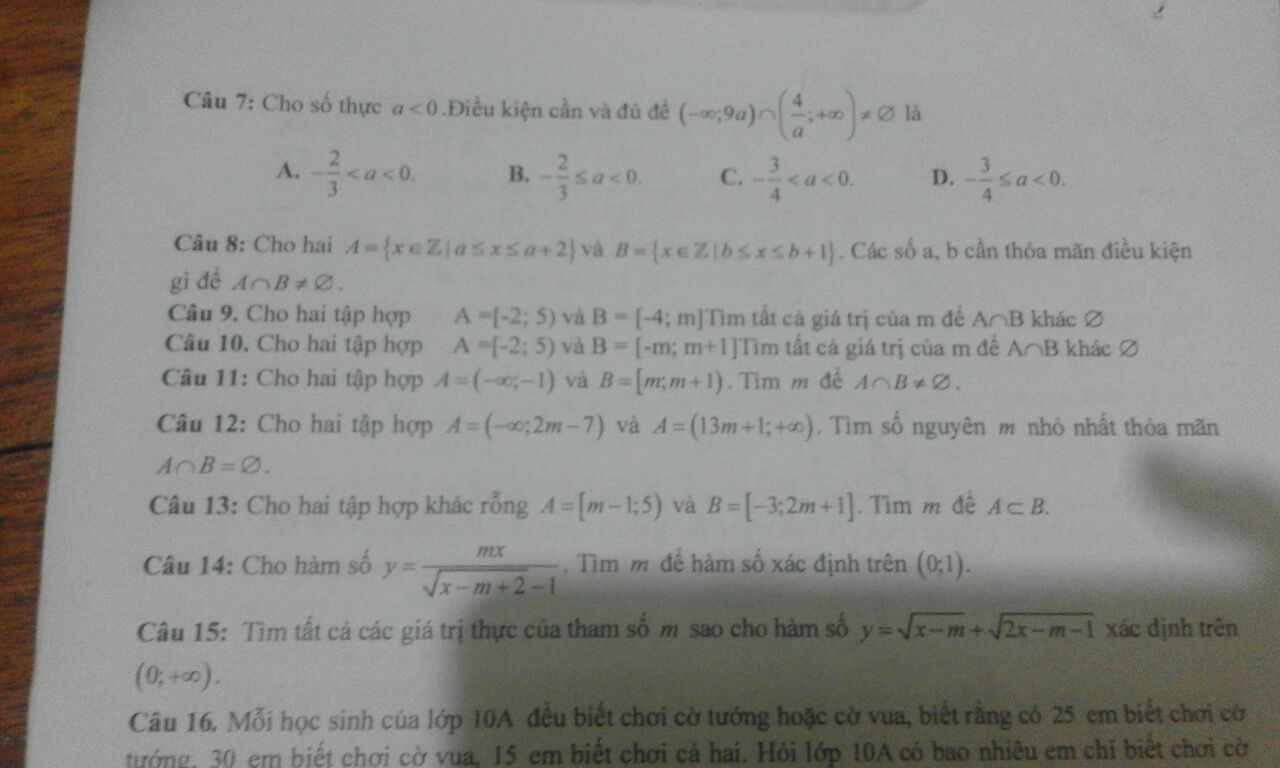 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!





Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
Vì AD là phân giác \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{15}{12+9}=\dfrac{15}{21}=\dfrac{5}{7}\Rightarrow BD=\dfrac{45}{7};CD=\dfrac{60}{7}cm\)
Xét tam giác ABC vuông tại A có DE vuông AC
=> DE // AB
Theo hệ quả Ta lét \(\dfrac{DC}{BC}=\dfrac{DE}{AB}\Rightarrow DE=\dfrac{DC.AB}{BC}=\dfrac{36}{7}cm\)
Bài 7: Chứng minh theo quy nạp:
-Khi n=3 thì mệnh đề trở thành:
\(4.5.6=120⋮2^3\)
-Giả sử mệnh đề đúng với n=k tức là:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\).
-Ta chứng minh mệnh đề cũng đúng với n=k+1 tức là:
\(\left(k+2\right)\left(k+3\right)\left(k+4\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Thật vậy, ta có:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^{k+1}\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)⋮2^{k+1}\).
\(\Rightarrow\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Vậy mệnh đề cũng đúng với n=k+1. Theo nguyên lý Quy nạp toán học, mệnh đề đúng với mọi n nguyên dương lớn hơn 0.