Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3

TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=> \(\left\{{}\begin{matrix}a>0\\\Delta'\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\left[-\left(m+1\right)\right]^2-4\left(m+1\right)\le0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m>-1\\m^2-2m-3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m>3\)
Vậy m>3 thì...

TH1: m + 1 = 0 <=> m = -1 thay vào bpt ta có: 4 > 0 với mọi số thực x
=> m = - 1 thỏa mãn
TH2: m \(\ne\)-1
bpt có tập nghiệm S = R
<=> \(\hept{\begin{cases}\Delta'\le0\\m+1>0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m+1\right)^2-4\left(m+1\right)\le0\\m>-1\end{cases}}\)
<=> \(\hept{\begin{cases}\left(m+1\right)\left(m-3\right)\le0\\m>-1\end{cases}}\Leftrightarrow-1< m\le3\)
Kết hợp 2 TH: ta có: \(-1\le m\le3\) thì bpt có tập nghiệm: S = R
Đặt ( m + 1 ).x2 - 2. ( m-1 ) .x + 4 \(\ge\)0 ( 1 )
+) TH1 : m+ 1 = 0 <=> m =-1 .Bất phương trình ( 1 ) trở thành 4 \(\ge\)0 \(\forall x\inℝ\)( luôn đúng ) ( *)
+) TH2 : m + 1 \(\ne\)0 <=> m \(\ne\)-1 .Bất phương trình ( 1 ) có tập nghiệm \(S=ℝ\)
<=> \(\hept{\begin{cases}a>0\\\Delta'\le0\end{cases}\Leftrightarrow\hept{\begin{cases}m+1>0\\\Delta'=m^2-2m-3\le0\end{cases}\Leftrightarrow}-1< m\le3\left(^∗^∗\right)}\)
Từ ( *) và ( **) ta suy ra : \(-1\le m\le3\)

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
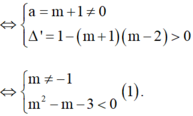
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
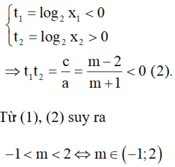

Đáp án B.
Đặt t = log 2 x , khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 ⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt ⇔ a = m + 1 ≠ 0 ∆ ' = 1 - m + 1 m - 2 > 0 ⇔ m ≠ - 1 m 2 - m - 3 < 0 1 .
Khi đó gọi x 1 ; x 2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x 1 < 1 < x 2 suy ra t 1 = log 2 x 1 < 0 t 2 = log 2 x 2 > 0 ⇒ t 1 t 2 = c a = m - 2 m + 1 < 0 2 .
Từ (1), (2) suy ra - 1 < m < 2 ⇔ m ∈ - 1 ; 2 là giá trị cần tìm.

Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2


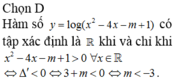
TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=> {a>0Δ′≤0⇔{m+1>0[−(m+1)]2−4(m+1)≤0{a>0Δ′≤0⇔{m+1>0[−(m+1)]2−4(m+1)≤0
<=>{m>−1m2−2m−3≥0⇔⎧⎪⎨⎪⎩m>−1[m<−1m>3⇔m>3{m>−1m2−2m−3≥0⇔{m>−1[m<−1m>3⇔m>3
Vậy m>3 thì...