Bài 1: Cho ABC cân tại A kẻ AH ⊥ BC (HBC)
a) Chứng minh: ∠ABH = ∠ABH suy ra AH là tia phân giác của ∠BAC
b) Kẻ HD ⊥ AB (D ∈ AB), HE ⊥ AC (E ∈ AC). Chứng minh ∠HDE cân.
c) Nếu cho AB = 29 cm, AH = 20 cm. Tính độ dài cạnh AB?
d) Chứng minh BC // DE.
e) Nếu cho ∠BAC = 1200 thì △HDE trở thành tam giác gì? Vì sao?
Bài 2: Cho tam giác ABC vuông tại A, có B = 60° và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E.
1/ Chứng minh: △ABD = △EBD.
2/ Chứng minh: △ABE là tam giác đều.
3/ Tính độ dài cạnh BC.
Bài 3: Cho tam giác ABC có AB = AC =10cm, BC = 12cm. Vẽ AH vuông góc BC tại H.
a) Chứng minh: △ABC cân.
b) Chứng minh △AHB = △AHC, từ đó chứng minh AH là tia phân giác của góc A.
c) Từ H vẽ HM ⊥ AB (M ∈ AB) và kẻ HN ⊥ AC (N ∈ AC).
Chứng minh : △BHM =△HCN
d) Tính độ dài AH.
e) Từ B kẻ Bx ⊥ AB, từ C kẻ Cy ⊥ AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm A thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a) Chứng minh △OAI = △OBI, IA = IB.
b) Cho biết OI = 10cm, AI = 6cm. Tính OA.
c) Gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. So sánh AK và BM?
d) Gọi C là giao điểm của OI và MK. Chứng minh OC vuông góc với MK
Bài 5: Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng
Héo mì pờ li mọi người ơi!!!!!!!!!!!!!!!!!!!!!! TvT - TvT - TvT - TvT - TvT - TvT - TvT


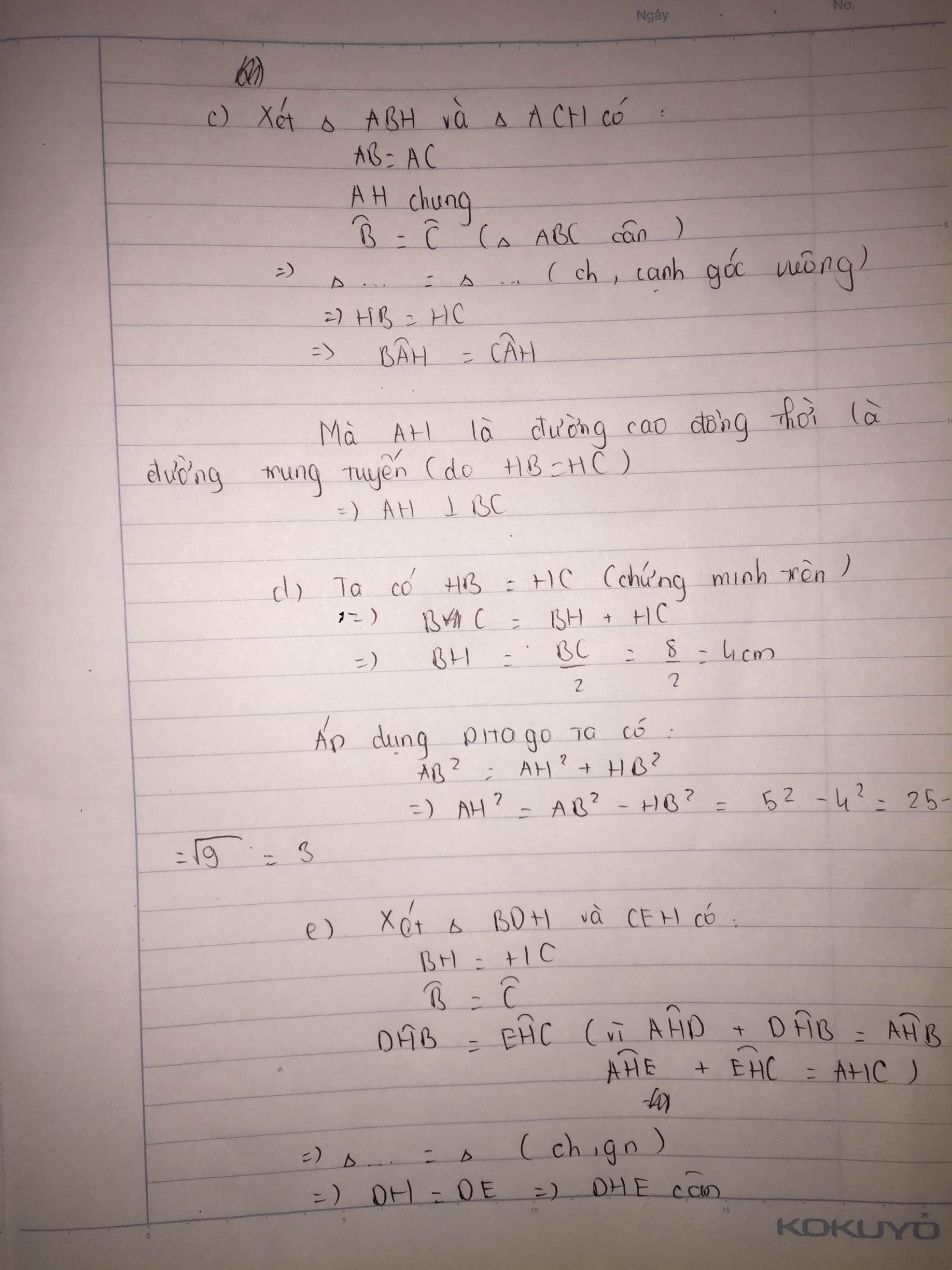
Bài 1:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHDB=ΔHEC
Suy ra; HD=HE
hay ΔHDE cân tại H
d: Xét ΔABC có BD/AB=CE/AC
nên DE//BC