Đổi 1 tấn = 1000kg

a) Công của cần trục:

A = P.h = mgh = 1000. 10.10 = 100000J

b) Công suất cần thiết của động cơ cần trục:

\(P_i=\dfrac{A}{t}=\dfrac{100000}{30}=3333,3W\)

Công suất của động cơ cần trục:

\(P=\dfrac{P_i}{H}=\dfrac{3333,3}{60\%}=5555,5W\)

c) Đổi 2 tấn = 2000kg

Công để nâng vật:

A' = F'.s = m'gh = 2000.10.10 = 200000J

Thời gian nâng vật:

\(A'=\dfrac{P}{t'}\Rightarrow t'=\dfrac{A'}{P}=\dfrac{200000}{5555,5}=36s\)

cảm mơn bạn nha

a,37500J

b,P=3750N

2,5kW = 2500W

15p = 900s

Công nâng vật là

\(A=P.t=2500.900=2,250,000\left(J\right)\) 

Trọng lượng của vật là

\(P=\dfrac{A}{h}=\dfrac{2,250,000}{10}=225,000\left(N\right)\) 

Khối lượng là

\(m=\dfrac{P}{10}=\dfrac{225,000}{10}=22500\left(kg\right)\)

a)Lên đều trong 20s:

   Công thực hiện: 

   \(A=P\cdot h=10m\cdot h=10\cdot20\cdot10=2000J\)

   Công suất: \(P=\dfrac{A}{t}=\dfrac{2000}{20}=100W\)

b)Vật chuyển động nhanh dần đều.

   Gia tốc a: \(S=\dfrac{1}{2}at^2\)

   \(\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot10}{4^2}=1,25\)m/s²

   Lực kéo F: 

    \(F=m\cdot a+mg=20\cdot1,25+20\cdot10=225N\)

   Công thực hiện: \(A=F\cdot s=225\cdot10=2250J\)

   Công suất: \(P=\dfrac{A}{t}=\dfrac{2250}{4}=562,5W\)

Vật chuyển động đều

ĐL 1 niuton: \(F=P=mg=1000.10=10000N\)

Công thực hiện của động cơ:

\(A=Pt\)

\(=> F.s=Pt\)

\(=> 10000.30=15000.t\)

\(=> t=20s\)

Đáp án B

Công cần thiết để kéo vật lên cao 50 m là:

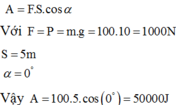
Công này chính là công mà động cơ điện đã cung cấp do vậy:

Công cần thiết để kéo vật lên cao 10 m là:

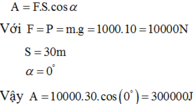
Công này chính là công mà động cơ điện đã cung cấp do vậy:

Đáp án A

Công cần thiết để kéo vật lên cao 10 m là: A = F.s.cosα

Với  F = P = mg = 1000.10 = 10000 N; s = 30 m; α = 0^o.

Suy ra A = 300000 J

Công này chính là công mà động cơ điện đã cung cấp do vậy:

cái công suất vật hình như là 250000 : 0,2 đúng không chị vì thời gian trên bài là o,2 ạ