1. Trong không gian có 3 điểm A(1;-2;4) B(3;1;2) C(0;1;1) a, tính vecto AB;BC suy ra độ dài cạnh AB,và BC b, viết phương trình mặt phẳng ABC c, tính khoảng cách từ điểm M(2;1;3) đến mặt phẳng (ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2018
Chọn C
Suy ra ABCD là hình bình hành.
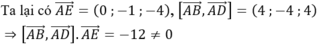
=>E.ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.
CM
20 tháng 7 2019
Chọn đáp án B
Gọi I là trung điểm AB và (P) là mặt phẳng trung trực của AB.
Ta có I là trung điểm AB nên I(-1;1;-2)
Lại có A B ⇀ = 4 ; - 8 ; - 6 và A B ⊥ P nên mặt phẳng (P) có một vectơ pháp tuyến là n ⇀ = 2 ; - 4 ; - 3 .
Phương trình mặt phẳng:
CM
27 tháng 7 2018
Đáp án C
A B → = ( 1 ; - 1 ; - 3 ) , D C → = ( 1 ; - 1 ; - 3 ) , A D → = ( 2 ; - 4 ; - 2 ) => ABCD là hình bình hành
A B → . A D → . A E → = 12 ⇒ E . A B C D là hình chóp đáy hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên
+ Mặt phẳng qua 4 trung điểm lần lượt là AD, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, EB, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, ED, AB, DC
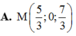
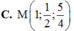
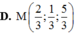
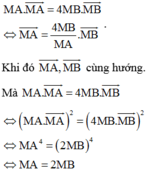
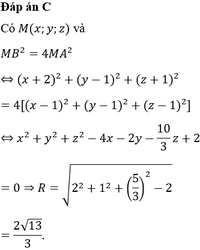
\(\overrightarrow{AB}=\left(2;3;2\right)\Rightarrow AB=\sqrt{2^2+3^2+2^2}=\sqrt{17}\)
\(\overrightarrow{BC}=\left(-3;0;-1\right)\Rightarrow BC=\sqrt{\left(-3\right)^2+0^2+\left(-1\right)^2}=\sqrt{10}\)
\(\left[\overrightarrow{AB};\overrightarrow{BC}\right]=\left(-3;-4;9\right)\)
Mặt phẳng (ABC) nhận (-3;-4;9) là 1 vtpt
Phương trình (ABC):
\(-3\left(x-1\right)-4\left(y+2\right)+9\left(z-4\right)=0\)
\(\Leftrightarrow-3x-4y+9z-41=0\)
\(d\left(M;\left(ABC\right)\right)=\dfrac{\left|-3.2+4.1+9.3-41\right|}{\sqrt{\left(-3\right)^2+\left(-4\right)^2+9^2}}=\dfrac{8\sqrt{106}}{53}\)