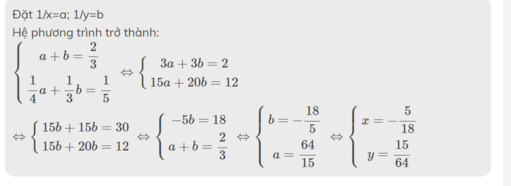
Đặt 1/x=a; 1/y=b

Hệ phương trình trở thành:

\(\left\{{}\begin{matrix}a+b=\dfrac{2}{3}\\\dfrac{1}{4}a+\dfrac{1}{3}b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=2\\15a+20b=12\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}15b+15b=30\\15b+20b=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-5b=18\\a+b=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{18}{5}\\a=\dfrac{64}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{18}\\y=\dfrac{15}{64}\end{matrix}\right.\)

a: =>2/x+2/y=2 và 4/x-2/y=1

=>6/x=3 và 1/x+1/y=1

=>x=2 và 1/y=1-1/2=1/2

=>x=2; y=2

b: Đặt 1/x=a; 1/y=b

=>1/3a+1/3b=1/4 và 5/6a+b=2/3

=>a=1/2; b=1/4

=>x=2; y=4

a: \(\left\{{}\begin{matrix}3x-2y=11\\4x-5y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=11+2y\\4x-5y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\4\left(\dfrac{2}{3}y+\dfrac{11}{3}\right)-5y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\\dfrac{8}{3}y+\dfrac{44}{3}-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\-\dfrac{7}{3}y=3-\dfrac{44}{3}=-\dfrac{35}{3}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=5\\x=\dfrac{2}{3}\cdot5+\dfrac{11}{3}=\dfrac{10}{3}+\dfrac{11}{3}=\dfrac{21}{3}=7\end{matrix}\right.\)

b: \(\left\{{}\begin{matrix}\dfrac{x}{2}-\dfrac{y}{3}=1\\5x-8y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}+1\\5x-8y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}y+2\\5\left(\dfrac{2}{3}y+2\right)-8y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+2\\\dfrac{10}{3}y+10-8y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{14}{3}y=3-10=-7\\x=\dfrac{2}{3}y+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=7:\dfrac{14}{3}=7\cdot\dfrac{3}{14}=\dfrac{3}{2}\\x=\dfrac{2}{3}\cdot\dfrac{3}{2}+2=3\end{matrix}\right.\)

c: \(\left\{{}\begin{matrix}3x+5y=1\\2x-y=-8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=2x+8\\3x+5\left(2x+8\right)=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x+8\\3x+10x+40=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=2x+8\\13x=-39\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-3\\y=2\cdot\left(-3\right)+8=8-6=2\end{matrix}\right.\)

d: \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{2}{3}\\x+y-10=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y\\x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3}y+y=10\\x=\dfrac{2}{3}y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{5}{3}y=10\\x=\dfrac{2}{3}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=\dfrac{2}{3}\cdot6=4\end{matrix}\right.\)

a.

ĐKXĐ: \(\left\{{}\begin{matrix}x\ge2\\y\ge3\end{matrix}\right.\)

\(\left\{{}\begin{matrix}3\sqrt{x-2}+3\sqrt{y-3}=9\\2\sqrt{x-2}-3\sqrt{y-3}=-4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}+3\sqrt{y-3}=9\\5\sqrt{x-2}=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}+3\sqrt{y-3}=9\\\sqrt{x-2}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-2}=1\\\sqrt{y-3}=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=7\end{matrix}\right.\)

b.

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne-1\\y\ne-4\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\dfrac{15x}{x+1}+\dfrac{10}{y+4}=20\\\dfrac{4x}{x+1}-\dfrac{10}{y+4}=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{15x}{x+1}+\dfrac{10}{y+4}=20\\\dfrac{19x}{x+1}=28\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+1}=\dfrac{28}{19}\\\dfrac{1}{y+4}=-\dfrac{4}{19}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}19x=28x+28\\4y+16=-19\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{28}{9}\\y=-\dfrac{35}{4}\end{matrix}\right.\)

a: =>xy-2x+2y-4=xy+y và 5xy+10x+y+2=5xy-10x-2y+4

=>-2x+y=4 và 20x+3y=2

=>x=-5/13; y=42/13

b: =>4x+2|y|=8 và 4x-3y=1

=>2|y|-3y=7 và 4x-3y=1

TH1: y>=0

=>2y-3y=7 và 4x-3y=1

=>-y=7 và 4x-3y=1

=>y=-7(loại)

TH2: y<0

=>-2y-3y=7 và 4x-3y=1

=>y=-7/5; 4x=1+3y=1-21/5=-16/5

=>x=-4/5; y=-7/5

1. \(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=5\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=9\end{matrix}\right.\) ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2y+xy^2+x+y=5xy\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^4y^2+x^2y^4+x^2+y^2=25x^2y^2\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\)\(\Leftrightarrow0=16x^2y^2\)

\(\Rightarrow\) phương trình vô nghiệm