Giúp mình câu này với huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường thẳng d có 1 vtpt là \(\left(1;-2\right)\)
Đường thẳng \(d'\) vuông góc d nên có 1 vtpt là (2;1) (đảo thứ tự tọa độ vtpt của d và đảo dấu 1 trong 2 vị trí tùy thích)
Phương trình d':
\(2\left(x+1\right)+1\left(y-1\right)=0\Leftrightarrow2x+y+1=0\)

a.
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+sinx.cosx\right)=1\)
Đặt \(sinx+cosx=t\) \(\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t\left(1+\dfrac{t^2-1}{2}\right)=1\)
\(\Leftrightarrow t^3+t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2+t+2\right)=0\)
\(\Leftrightarrow t=1\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)
b.
Đặt \(sinx-cosx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Phương trình trở thành:
\(t^3=1+\dfrac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)

Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2



b: (d) có hệ số góc bằng 1 nên (d): y=x+b
f(2)=-1/2*2^2=-2
Thay x=2 và y=-2 vào (d), ta được:
b+2=-2
=>b=-4
a: 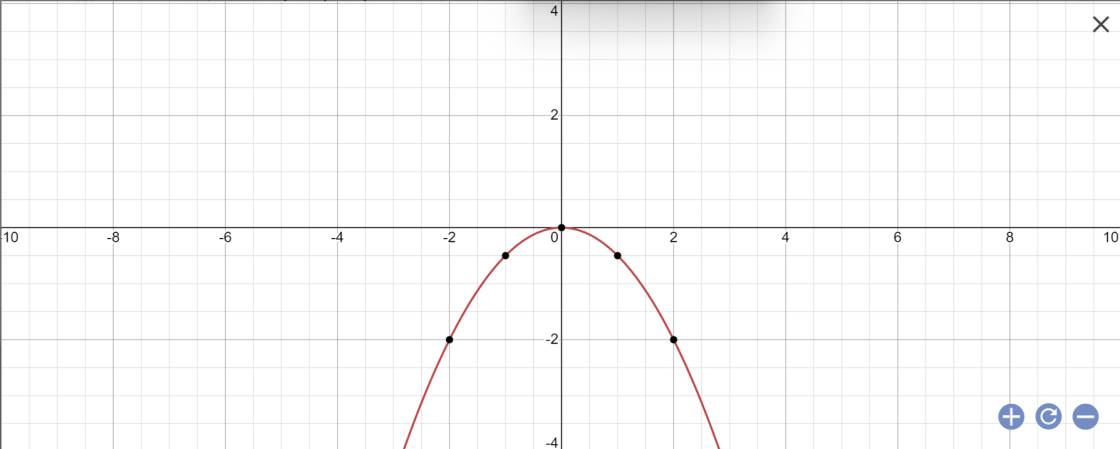







\(\Delta'=3-\left(-6\right)=9>0\)
vậy pt có 2 nghiệm pb
\(x_1=\sqrt{3}-3;x_2=\sqrt{3}+3\)