Cho tam giác ABC vuông tại A có AB = 5cm, AC = 12cm.
aTính BC.
b. Kéo dài AB lấy D sao cho B là trung điểm của AD. Nối CD, qua B vẽ đường thẳng vuông góc với AD cắt CD tại E.
Chứng minh ΔABE = ΔDBE và suy ra ΔAED cân.
c. Kẻ AK vuông góc với BC tại K. Qua D kẻ đường thẳng vuông góc với đường thẳng CB tại F. Chứng minh B là trung điểm của KF.
d. Chứng minh ΔAEC cân và suy ra E là trung điểm của DC.


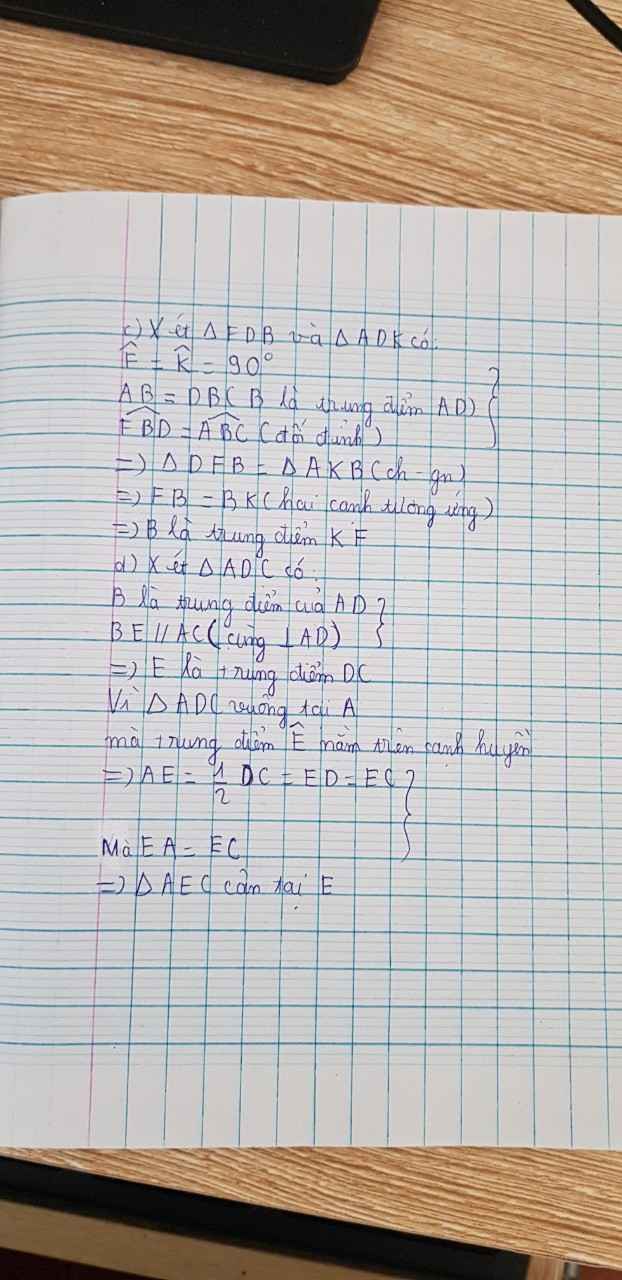

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay \(BC=13cm\)
Vậy: BC=13cm
b) XÉT ΔABE VÀ ΔDBE ,CÓ
BD=BA (B LÀ TRUNG ĐIỂM CỦA AD)
\(\widehat{DBE}=\widehat{ABE}\) =90
EB : CẠNH CHUNG
⇒ΔABE = ΔDBE (C-G-C)