Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D và trên tia đối của tia CA lấy điểm E sao
cho CE = BD. Chứng minh rằng: BC < DE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
16 tháng 2 2019
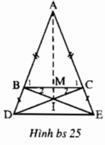
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.

15 tháng 4 2021
- doandieungoc
- 30/06/2020
Đáp án:
Giải thích các bước giải:
Xét ΔACD và ΔACDcó:
Góc DCE là góc ngoài đỉnh C của tam giác ấy, nên:
DCE^>CDA^
DCE^>CDA^
Hai tam giác BCD và EDC có hai cạnh bằng nhau từng đôi một
BD = EC (theo giả thiết)
CD là cạnh chung
Hai góc xen giữa hai cạnh ấy không bằng nhau
DCE^ >^CDB
DCE^>CDB^
=> hai cạnh đối diện với hai góc ấy không bằng nhau.
Ta suy ra: BC < DE.