giúp e với ạ e cần gấp e cảm ơn rất nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
b: AC=12cm
AH=7,2cm
Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/9=CD/15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{9}=\dfrac{CD}{15}=\dfrac{AD+CD}{9+15}=\dfrac{12}{24}=\dfrac{1}{2}\)
Do đó: AD=4,5cm; CD=7,5cm

Xét tam giác MNP có MP là đường phân giác của \(\widehat{MNP}\) ta có:
\(\dfrac{MN}{NP}=\dfrac{MF}{FP}\Leftrightarrow\dfrac{MN}{NP}=\dfrac{MF}{MP-MF}\Leftrightarrow\dfrac{6}{10}=\dfrac{MF}{8-MF}\Rightarrow MF=3\left(cm\right)\)\(\Rightarrow FP=8-3=5\left(cm\right)\)
Xét tam giác MNP có ME là đường cao ứng với cạnh huyền, ta có: \(\dfrac{1}{ME^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\Leftrightarrow\dfrac{1}{ME^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\Rightarrow ME=4,8\left(cm\right)\)

a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)


bạn tham khảo lấy ý làm bài nha
Cộng hòa xã hội chủ nghĩa Việt Nam
Độc lập- Tự do- Hạnh phúc
Hà Nội, ngày 14 tháng 5 năm 2021
BẢN ĐỀ NGHỊ
Kính gửi: cô chủ nhiệm lớp 7B
Tên em là: Nguyễn Văn A
Chức vụ: Lớp trưởng
Lí do viết đơn: Hiện nay, lớp ta thường xuyên mắc lỗi. Từ lỗi nề nếp đi học muộn, nói chuyện giờ truy bài đến việc không làm bài tập. Những lỗi sai ấy chủ yếu do một nhóm bạn thuộc tổ bốn gây nên và đã, đang ảnh hưởng rất nhiều đến thi đua của lớp. Vì thế, em viết đơn này đề nghị cô chuyển chỗ cho các bạn và có biện pháp lâu dài nhắc nhở để lớp tiến bộ, đi lên.
Em xin chân thành cảm ơn!
Lớp trưởng
A
Nguyễn Văn A

`A=1/(x+sqrtx)+(2sqrtx)/(x-1)-1/(x-sqrtx)`
`=(sqrtx-1+2x-sqrtx-1)/(sqrtx(x-1))`
`=(2x-2)/(sqrtx(x-1))`
`=2/sqrtx`
`b)A=1`
`<=>2/sqrtx=1`
`<=>sqrtx=2`
`<=>x=4(tm)`

- Nửa cầu Bắc nằm phía trên đường xích đạo.
- Nửa cầu Nam nằm phía dưới đường xích đạo.
- Các vĩ tuyến Bắc là các vĩ tuyến nằm từ xích đạo đến cực Bắc.
- Các vĩ tuyến Nam là các vĩ tuyến nằm từ xích đạo đến cực Nam.

a.
Ta có: MN//BC (gt)
Áp dụng định lý Ta-lét, ta có:
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
\(\Leftrightarrow\dfrac{1,2}{3}=\dfrac{AN}{4}\)
\(\Leftrightarrow3AN=4,8\)
\(\Leftrightarrow AN=1,6cm\)
b.Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=\sqrt{25}=5cm\)
Áp dụng t/c đường phân giác góc A, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{CD}{4}=\dfrac{BD}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{CD}{4}=\dfrac{BD}{3}=\dfrac{CD+BD}{4+3}=\dfrac{5}{7}\)
\(\Rightarrow CD=\dfrac{5}{7}.4=\dfrac{20}{7}cm\)
\(\Rightarrow BD=\dfrac{5}{7}.3=\dfrac{15}{7}cm\)





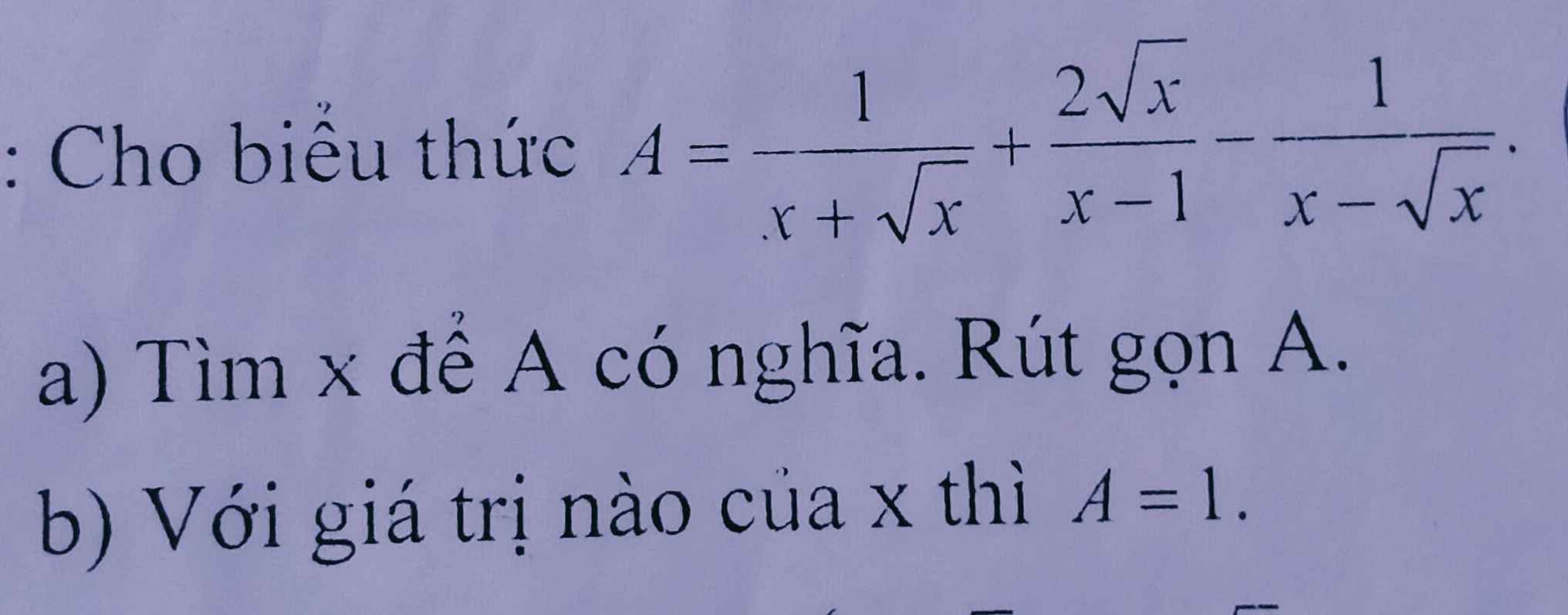


a: \(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/9=CD/15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{9}=\dfrac{CD}{15}=\dfrac{AD+CD}{9+15}=\dfrac{12}{24}=\dfrac{1}{2}\)
Do đó: AD=4,5(cm); CD=7,5(cm)
b: Xét ΔABC có DE//AB
nên DE/AB=CD/CA
=>DE/9=7,5/12
=>DE/9=5/8
hay DE=45/8(cm)