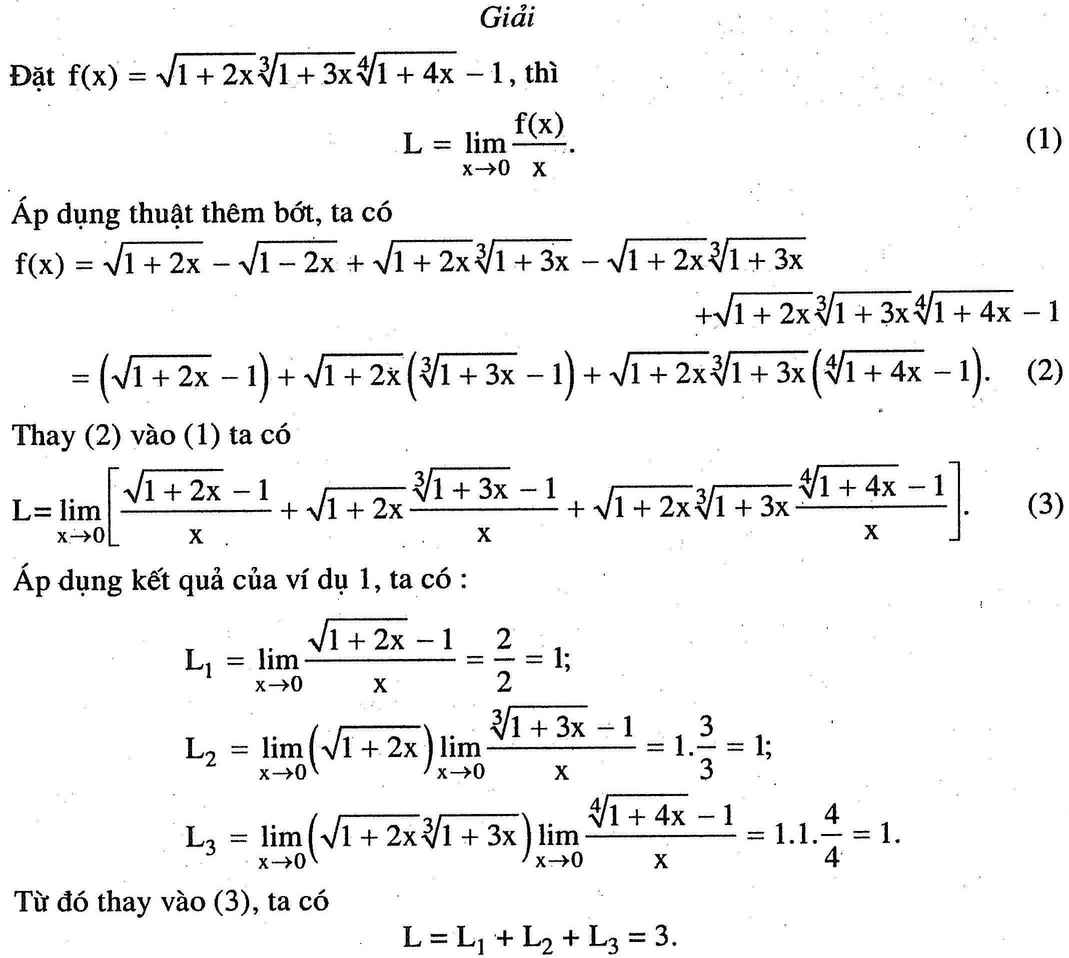
Ta xét:

\(\sqrt{1+2x}\cdot\sqrt[3]{1+3x}-1\)

\(=\sqrt{1+2x}-\sqrt{1+2x}+\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1\)

\(=\left(\sqrt{1+2x}-1\right)+\sqrt{1+2x}\cdot\left(\sqrt[3]{1+2x}-1\right)\)

Xét giới hạn trên:

\(\Rightarrow^{lim}_{x\rightarrow0}\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}\)

   \(=^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}-1}{x}\right)+^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}\cdot\left(\sqrt[3]{1+2x}-1\right)}{3}\right)\)

Tính giới hạn từng thành phần:

* \(^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}-1}{x}\right)=^{lim}_{x\rightarrow0}\left(\dfrac{1+2x-1}{x\left(\sqrt{1+2x}+1\right)}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\dfrac{2}{\sqrt{1+2x}+1}\right)=\dfrac{2}{\sqrt{1+2\cdot0}+1}=1\left(1\right)\)

* \(^{lim}_{x\rightarrow0}\left(\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\sqrt{1+2x}\cdot\dfrac{1+2x-1}{x\left(\left(\sqrt[3]{1+2x}\right)^2+\sqrt[3]{1+2x}+1\right)}\right)\)

  \(=^{lim}_{x\rightarrow0}\left(\sqrt{1+2x}\cdot\dfrac{2}{\left(\sqrt[3]{1+2x}\right)^2+\sqrt[3]{1+2x}+1}\right)\)

  \(=\sqrt{1+2\cdot0}\cdot\dfrac{2}{(\sqrt[3]{1+2\cdot0})^2+\sqrt[3]{1+2\cdot0}+1}\)

  \(=\dfrac{2}{3}\left(2\right)\)

Lấy \(\left(1\right)+\left(2\right)\) ta được:

\(^{lim}_{x\rightarrow0}\dfrac{\sqrt{1+2x}\cdot\sqrt[3]{1+2x}-1}{x}=1+\dfrac{2}{3}=\dfrac{5}{3}\)

\(a=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-1+1-\sqrt[3]{2x+1}}{x}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{4x}{\sqrt[]{4x+1}+1}+\dfrac{-2x}{1+\sqrt[3]{2x+1}+\sqrt[3]{\left(2x+1\right)^2}}}{x}\)

\(=\lim\limits_{x\rightarrow0}\left(\dfrac{4}{\sqrt[]{4x+1}+1}+\dfrac{-2}{1+\sqrt[3]{2x+1}+\sqrt[3]{\left(2x+1\right)^2}}\right)=...\)

\(b=\lim\limits_{x\rightarrow1}\dfrac{4\left(x-1\right)\left(\sqrt[3]{\left(5x+3\right)^2}+2\sqrt[3]{5x+3}+4\right)}{5\left(x-1\right)\left(\sqrt[]{4x+5}+3\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{4\left(\sqrt[3]{\left(5x+3\right)^2}+2\sqrt[3]{5x+3}+4\right)}{5\left(\sqrt[]{4x+5}+3\right)}=...\)

\(c=\lim\limits_{x\rightarrow-1}\dfrac{\left(2x+3\right)^{\dfrac{1}{4}}+\left(2+3x\right)^{\dfrac{1}{3}}}{\left(x+2\right)^{\dfrac{1}{2}}-1}\)

\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{1}{2}\left(2x+3\right)^{-\dfrac{3}{4}}+\left(2+3x\right)^{-\dfrac{2}{3}}}{\dfrac{1}{2}\left(x+2\right)^{-\dfrac{1}{2}}}=3\)

Tui nghĩ cái này L'Hospital chứ giải thông thường là ko ổn :)

\(M=\lim\limits_{x\rightarrow0}\dfrac{\left(1+4x\right)^{\dfrac{1}{2}}-\left(1+6x\right)^{\dfrac{1}{3}}}{1-\cos3x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2}\left(1+4x\right)^{-\dfrac{1}{2}}.4-\dfrac{1}{3}\left(1+6x\right)^{-\dfrac{2}{3}}.6}{3.\sin3x}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{-\dfrac{1}{4}.4\left(1+4x\right)^{-\dfrac{3}{2}}.4+\dfrac{2}{9}.6.6\left(1+6x\right)^{-\dfrac{5}{3}}}{3.3.\cos3x}\) 

Giờ thay x vô là được

\(N=\lim\limits_{x\rightarrow0}\dfrac{\left(1+ax\right)^{\dfrac{1}{m}}-\left(1+bx\right)^{\dfrac{1}{n}}}{\left(1+x\right)^{\dfrac{1}{2}}-1}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{m}.\left(1+ax\right)^{\dfrac{1}{m}-1}.a-\dfrac{1}{n}\left(1+bx\right)^{\dfrac{1}{n}-1}.b}{\dfrac{1}{2}\left(1+x\right)^{-\dfrac{1}{2}}}=\dfrac{\dfrac{a}{m}-\dfrac{b}{n}}{\dfrac{1}{2}}\)

\(V=\lim\limits_{x\rightarrow0}\dfrac{\left(1+mx\right)^n-\left(1+nx\right)^m}{\left(1+2x\right)^{\dfrac{1}{2}}-\left(1+3x\right)^{\dfrac{1}{3}}}=\lim\limits_{x\rightarrow0}\dfrac{n\left(1+mx\right)^{n-1}.m-m\left(1+nx\right)^{m-1}.n}{\dfrac{1}{2}\left(1+2x\right)^{-\dfrac{1}{2}}.2-\dfrac{1}{3}\left(1+3x\right)^{-\dfrac{2}{3}}.3}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{n\left(n-1\right)\left(1+mx\right)^{n-2}.m-m\left(m-1\right)\left(1+nx\right)^{m-2}.n}{-\dfrac{1}{2}\left(1+2x\right)^{-\dfrac{3}{2}}.2+\dfrac{2}{9}.3.3\left(1+3x\right)^{-\dfrac{5}{3}}}=....\left(thay-x-vo-la-duoc\right)\)

\(a=\lim\limits_{x\rightarrow3}\dfrac{2x+3-x^2}{\left(x^2-4x+3\right)\left(\sqrt[]{2x+3}+x\right)}=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(-x-1\right)}{\left(x-3\right)\left(x-1\right)\left(\sqrt[]{2x+3}+x\right)}\)

\(=\lim\limits_{x\rightarrow3}\dfrac{-x-1}{\left(x-1\right)\left(\sqrt[]{2x+3}+x\right)}=...\)

\(b=\lim\limits_{x\rightarrow0}\dfrac{\left(x+1\right)^{\dfrac{1}{3}}-1}{\left(2x+1\right)^{\dfrac{1}{4}}-1}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{3}\left(x+1\right)^{-\dfrac{2}{3}}}{\dfrac{1}{2}\left(2x+1\right)^{-\dfrac{3}{4}}}=\dfrac{2}{3}\)

\(c=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt[]{1+4x}-2x-1\right)+\left(2x+1-\sqrt[3]{1+6x}\right)}{x^2}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{-4x^2}{2x+1+\sqrt[]{4x+1}}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{1+6x}+\sqrt[3]{\left(1+6x\right)^2}}}{x^2}\)

\(=\lim\limits_{x\rightarrow0}\left(\dfrac{-4}{2x+1+\sqrt[]{4x+1}}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{1+6x}+\sqrt[3]{\left(1+6x\right)^2}}\right)=...\)

\(\dfrac{\sqrt{1+2x}\sqrt[3]{1+3x}\sqrt[4]{1+4x}-1}{x}\)

\(=\dfrac{\sqrt[3]{1+3x}\sqrt[4]{1+4x}\left(\sqrt{1+2x}-1\right)}{x}+\dfrac{\sqrt[4]{1+4x}\left(\sqrt[3]{1+3x}-1\right)}{x}+\dfrac{\sqrt[4]{1+4x}+1}{x}\)

Dùng L'Hopital dễ dàng chứng minh với mọi n nguyên dương ta có:

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt[n]{1+nx}-1}{x}=\lim\limits_{x\rightarrow0}\dfrac{\left(1+nx\right)^{\dfrac{1}{n}}-1}{x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{n}n\left(1+nx\right)^{\dfrac{1-n}{n}}}{1}=\dfrac{n}{n}=1\)

\(\Rightarrow\) giới hạn đã cho bằng \(\sqrt[3]{1+3.0}\sqrt[4]{1+4.0}.1+\sqrt[4]{1+4.0}.1+1=1+1+1=3\)

\(A=\lim\limits_{x\rightarrow0}\frac{\left(x+1\right)^{\frac{1}{3}}-1}{\left(2x+1\right)^{\frac{1}{4}}-1}=\lim\limits_{x\rightarrow0}\frac{\frac{1}{3}\left(x+1\right)^{-\frac{2}{3}}}{\frac{1}{2}\left(2x+1\right)^{-\frac{3}{4}}}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}\)

\(B=\lim\limits_{x\rightarrow7}\frac{\sqrt[3]{4x-1}\sqrt{x-2}}{\sqrt[4]{2x+2}-2}=\frac{3\sqrt{5}}{0}=+\infty\)

\(C=\lim\limits_{x\rightarrow0}\frac{\sqrt{\left(3x+1\right)\left(4x+1\right)}\left(\sqrt{2x+1}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{4x+1}\left(\sqrt{3x+1}-1\right)}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{4x+1}-1}{x}\)

Xét \(\lim\limits_{x\rightarrow0}\frac{\sqrt{ax+1}-1}{x}=\lim\limits_{x\rightarrow0}\frac{\left(ax+1\right)^{\frac{1}{2}}-1}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{a}{2}\left(ax+1\right)^{-\frac{1}{2}}}{1}=\frac{a}{2}\)

\(\Rightarrow C=\frac{2}{2}+\frac{3}{2}+\frac{4}{2}=\frac{9}{2}\)

\(D=\lim\limits_{x\rightarrow0}\frac{\left(1+4x\right)^{\frac{1}{2}}-\left(1+6x\right)^{\frac{1}{3}}}{x^2}=\lim\limits_{x\rightarrow0}\frac{2\left(1+4x\right)^{-\frac{1}{2}}-2\left(1+6x\right)^{-\frac{2}{3}}}{2x}\)

\(D=\lim\limits_{x\rightarrow0}\frac{-2\left(1+4x\right)^{-\frac{3}{2}}+4\left(1+6x\right)^{-\frac{5}{3}}}{1}=-2+4=2\)

\(E=\lim\limits_{x\rightarrow0}\frac{\left(1+ax\right)^{\frac{1}{n}}-\left(1+bx\right)^{\frac{1}{n}}}{x}=\lim\limits_{x\rightarrow0}\frac{\frac{a}{n}\left(1+ax\right)^{\frac{1-n}{n}}-\frac{b}{n}\left(1+bx\right)^{\frac{1-n}{n}}}{1}=\frac{a-b}{n}\)

Vì câu đó ko phải dạng vô định, nó là 1 giới hạn bình thường.

Mình đoán bạn ghi nhầm đề, đề bài là \(\lim\limits_{x\rightarrow7}\frac{\sqrt[3]{4x-1}-\sqrt{x+2}}{\sqrt[4]{2x+2}-2}\) thì hợp lý hơn, đây là 1 giới hạn vô định \(\frac{0}{0}\)

\(a=\lim\limits_{x\rightarrow2}\dfrac{\left(x^2-x-2\right)\left(x^2+x\sqrt[3]{3x+2}+\sqrt[3]{\left(3x+2\right)^2}\right)}{\left(x^3-3x-2\right)\left(x+\sqrt[]{x+2}\right)}\)

\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+1\right)\left(x^2+x\sqrt[3]{3x+2}+\sqrt[3]{\left(3x+2\right)^2}\right)}{\left(x-2\right)\left(x+1\right)^2\left(x+\sqrt[]{x+2}\right)}\)

\(=\lim\limits_{x\rightarrow2}\dfrac{x^2+x\sqrt[3]{3x+2}+\sqrt[3]{\left(3x+2\right)^2}}{\left(x+1\right)\left(x+\sqrt[]{x+2}\right)}=...\)

\(b=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt[]{1+2x}-x-1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^3+3x^2}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)

\(=\lim\limits_{x\rightarrow0}\left(\dfrac{1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)

\(=...\)

\(c=\lim\limits_{x\rightarrow-1}\dfrac{\left(\sqrt[]{5+4x}-2x-3\right)+\left(2x+3-\sqrt[3]{7+6x}\right)}{x^3+x^2-x-1}\)

\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{5+4x-\left(2x+3\right)^2}{2x+3+\sqrt[]{5+4x}}+\dfrac{\left(2x+3\right)^3-\left(7+6x\right)}{\left(2x+3\right)^2+\left(2x+3\right)\sqrt[3]{7+6x}+\sqrt[3]{\left(7+6x\right)^2}}}{\left(x-1\right)\left(x+1\right)^2}\)

\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{-4\left(x+1\right)^2}{2x+3+\sqrt[]{5+4x}}+\dfrac{\left(x+1\right)^2\left(8x+20\right)}{\left(2x+3\right)^2+\left(2x+3\right)\sqrt[3]{7+6x}+\sqrt[3]{\left(7+6x\right)^2}}}{\left(x-1\right)\left(x+1\right)^2}\)

\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{-4}{2x+3+\sqrt[]{5+4x}}+\dfrac{8x+20}{\left(2x+3\right)^2+\left(2x+3\right)\sqrt[3]{7+6x}+\sqrt[3]{\left(7+6x\right)^2}}}{x-1}\)

\(=...\)

\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+3x^2}-\sqrt{x^2-2x}\right)\)

\(=\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{x^3+3x^2}-x+x-\sqrt{x^2-2x}\right)\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x^3+3x^2-x^3}{\sqrt[3]{\left(x^3+3x^2\right)^3}+x\cdot\sqrt[3]{x^3+3x^2}+x^2}+\dfrac{x^2-x^2+2x}{x+\sqrt{x^2-2x}}\)

\(=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{3x^2}{\sqrt[3]{\left(x^3+3x^2\right)^3}+x\cdot\sqrt[3]{x^3+3x^2}+x^2}+\dfrac{2x}{x+\sqrt{x^2-2x}}\right)\)

\(=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{3}{\sqrt[3]{\left(1+\dfrac{3}{x}\right)^3}+\sqrt[3]{1+\dfrac{3}{x}}+\dfrac{1}{x}}+\dfrac{2}{1+\sqrt{1-\dfrac{2}{x}}}\right)\)

\(=\dfrac{3}{1+1+1}+\dfrac{2}{1+1}\)

=1+1

=2