Cho tam giác ABC vuống tại B có AB=6cm,AC=10cm,và đường cao BH.
a)Tính BC,diện tích tam giác ABC
b)Chứng minh:tam giác BAH và tam giác ABC đồng dạng và tính BH,AH,HC
c)Chúng minh:tam giác BHA và tam giác HBC đồng dạng
GIÚP MÌNH BÀI NÀY VỚI,MÌNH CẦN GẤP Ạ


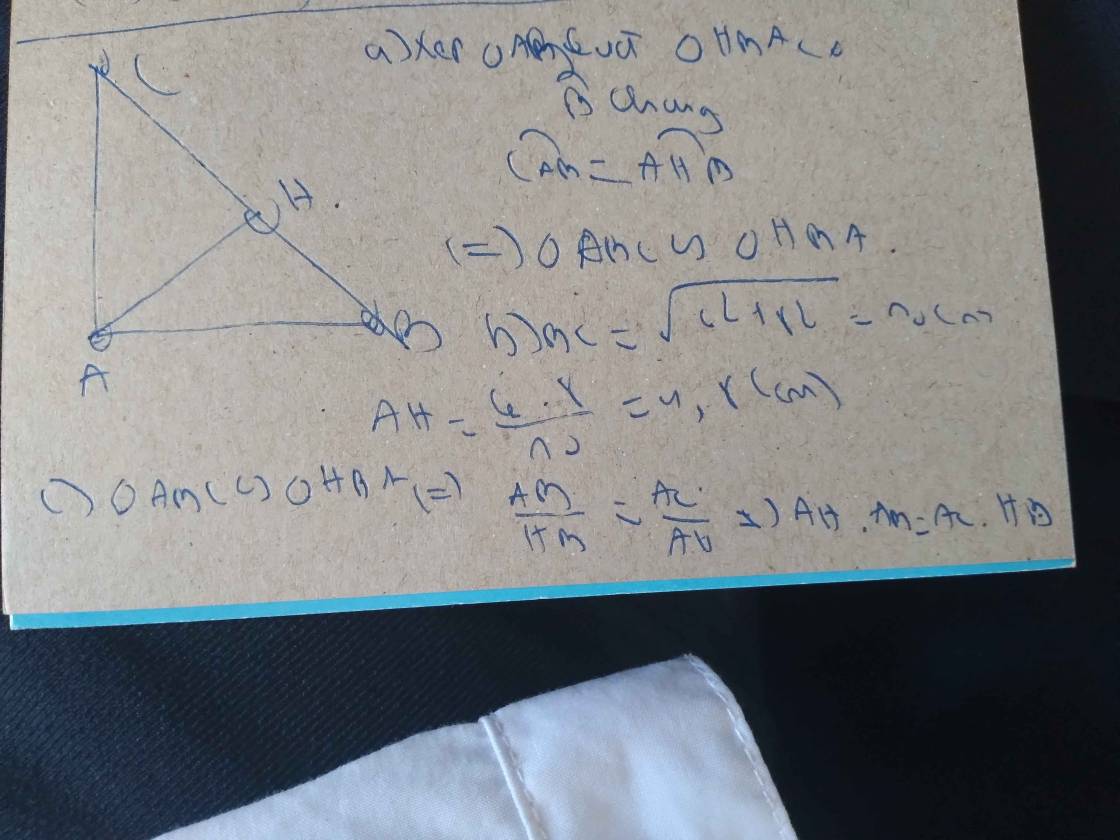

a.Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(AC^2=BA^2+BC^2\)
\(\Rightarrow BC=\sqrt{AC^2-BA^2}=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
\(S_{ABC}=\dfrac{1}{2}.BA.BC=\dfrac{1}{2}.6.8=24cm^2\)
b.Xét tam giác BAH và tam giác ABC, có:
\(\widehat{B}=\widehat{H}=90^o\)
Góc A: chung
Vậy tam giác BAH đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{BH}{BC}=\dfrac{AB}{AC}\)
\(\Leftrightarrow\dfrac{BH}{8}=\dfrac{6}{10}\)
\(\Leftrightarrow10BH=48\Leftrightarrow BH=4,8cm\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6cm\)
Áp dụng định lý pitago vào tam giác vuông ACH, có:
\(BC^2=CH^2+BH^2\)
\(\Rightarrow CH=\sqrt{BC^2-BH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4cm\)
c. Xét tam giác BHA và tam giác BHC, có:
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(\widehat{ACH}=\widehat{BAH}\) ( cùng phụ với góc B )
Vậy tam giác BHA đồng dạng tam giác BHC ( g.g )
a) -Xét △ABC vuông tại B:
\(AB^2+BC^2=AC^2\) (định lí Py-ta-go)
\(\Rightarrow BC=\sqrt{AC^2-AB^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{ABC}=\dfrac{AB.BC}{2}=\dfrac{6.8}{2}=24\left(cm^2\right)\)
b) -Xét △BAH và △ABC:
\(\widehat{AHB}=\widehat{ABC}=90^0\)
\(\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△BAH∼△CAB (g-g)
\(\Rightarrow\dfrac{BH}{CB}=\dfrac{AH}{AB}=\dfrac{BA}{CA}\)
\(\Rightarrow BH=\dfrac{BA.CB}{CA}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
\(AH=\dfrac{BA.AB}{CA}=\dfrac{6.6}{10}=3,6\left(cm\right)\)
\(HC=AC-AH=10-3,6=6,4\left(cm\right)\)
c) -Xét △BHA và △HBC:
\(\widehat{BHA}=\widehat{BHC}=90^0\)
\(\widehat{ABH}=\widehat{HCB}\)(△BAH∼△CAB)
\(\Rightarrow\)△BHA∼△CHB (g-g)