Cho hình thang ABCD (AB//CD), kẻ xy// AB. tia xy giao AD tại M, giao BC tại N. Biết diện tích tứ giác ABNM bằng diện tích tứ giác MNCD, AB=9 cm, CD=15cm . Tính MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:
Suy ra: MN// AB// CD và
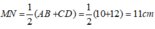
Suy ra: tứ giác MNCD là hình thang.
Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:
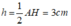
Diện tích hình thang ABNM là :
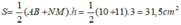
Chọn đáp án D

Ta có: M là TĐ của AD và N là TĐ của BC
=> MN là đường trung bình của hình thang ABCD
=> \(\left\{{}\begin{matrix}MN//AB\\MN=\dfrac{AB+CD}{2}\end{matrix}\right.\)
Ta có: MN // AB => tứ giác ABNM là hình thang
Ta có: AB = ( MN x 2 ) - CD = 20 - 12 = 8 cm
Ta có: Gọi O là gđ của MN và AH
=> AO là đường cao của hình thang ABCD và AO = 1/2 AH => AO = 3 cm
Diện tích hình thang ABMN là:
\(\dfrac{\left(8+10\right).3}{2}=27\) cm vuông