Bài 1: Cho tứ giác MNPQ biết góc M chia góc N chia góc P chia góc Q = 1/2/3/4
a) Tính các góc M, N, P, Q
b) Chứng minh: MN song song với PQ
c) Gọi R là giao điểm của MQ và NP. Tính các góc của Tam giác PQR
(Câu a em làm đc rồi ạ, còn câu b với câc c, giúp em với!)
Thanks nhiều ạ


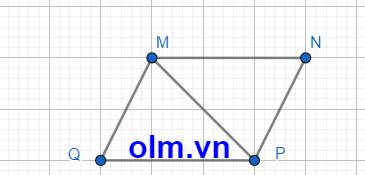
a. Ta thấy góc \(M+Q=36^0+144^0=180^0\), \(P+N=108^0+72^0=180^0\)
Vậy MN // PQ.
b. Góc RQP = góc M = \(36^0\)
\(RPQ=PNM=72 ^0\)
Góc \(QRP=180^0-36^0-72^0=72^0\)