Cho đường tròn $(O)$ đường kính $AB$. Lấy điểm $C$ thuộc đoạn $AO$ ($C$ không trùng $O$ và $A$), vẽ đường tròn $(O')$ đường kính $CB$. Qua trung điểm $M$ của $AC$, kẻ đường thẳng vuông góc với $AC$, cắt $(O)$ tại $D$ và $E$. Gọi $I$ là giao điểm thứ hai của $BD$ với đường tròn $(O')$, $J$ là giao điểm thứ hai của $BE$ với đường tròn $(O')$. Chứng minh:
a) Tứ giác $CDAE$ là hình thoi.
b)...
Đọc tiếp
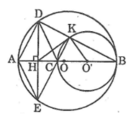
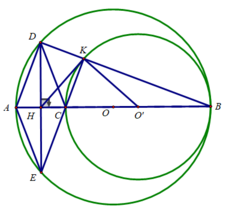
Cho đường tròn $(O)$ đường kính $AB$. Lấy điểm $C$ thuộc đoạn $AO$ ($C$ không trùng $O$ và $A$), vẽ đường tròn $(O')$ đường kính $CB$. Qua trung điểm $M$ của $AC$, kẻ đường thẳng vuông góc với $AC$, cắt $(O)$ tại $D$ và $E$. Gọi $I$ là giao điểm thứ hai của $BD$ với đường tròn $(O')$, $J$ là giao điểm thứ hai của $BE$ với đường tròn $(O')$. Chứng minh:
a) Tứ giác $CDAE$ là hình thoi.
b) $CI//AD$.
c) Ba điểm $E$, $C$, $I$ thẳng hàng.
d) Bốn điểm $M$, $I$, $B$, $E$ cùng thuộc một đường tròn.
e) Ba đường thẳng $AM$, $DJ$, $EI$ đồng quy.
Vì cung ACAC có số đo 50∘50∘ nên ˆAOC=50∘AOC^=50∘
Vì AO⊥CD;AO//DE⇒CD⊥DEAO⊥CD;AO//DE⇒CD⊥DE⇒ˆCDE=90∘⇒CDE^=90∘ mà C,D,E∈(O)C,D,E∈(O) nên CECE là đường kính hay C;O;EC;O;E thẳng hàng
Xét (O)(O) có OAOA là đường cao trong tam giác cân ODCODC nên OAOA cũng là đường phân giác ⇒ˆCOA=ˆAOD=50∘⇒COA^=AOD^=50∘
Lại thấy ˆBOE=ˆAOC=50∘BOE^=AOC^=50∘ (đối đỉnh) suy ra ˆAOC=ˆAOD=ˆBOE=50∘AOC^=AOD^=BOE^=50∘ (D đúng) và suy ra cung ACAC bằng cung BEBE nên B đúng.
Ta có ˆDOE=180∘−ˆAOD−ˆBOE=80∘DOE^=180∘−AOD^−BOE^=80∘ nên cung AD<AD< cung DE⇒AD<DEDE⇒AD<DE hay đáp án A sai.
Lại có ˆAOE=ˆAOD+ˆDOE=50∘+80∘=130∘AOE^=AOD^+DOE^=50∘+80∘=130∘ và ˆBOD=ˆBOE+ˆDOE=50∘+80∘=130∘BOD^=BOE^+DOE^=50∘+80∘=130∘
Nên ˆAOE=ˆBODAOE^=BOD^ suy ra số đo cung AE=AE= số đo cung BD.BD. Do đó C đúng.
Phương án B, C, D đúng và A sai.