Số đo góc D là: 360^o - 65^o - 117^o - 68^o = 110^o

Số đo góc ngoài đỉnh D: 180^o - 110^o = 70^o

Số đo góc ngoài tại đỉnh D là:

\(180^0-\left(360^0-65^0-117^0-68^0\right)=70^0\)

Số đo góc ngoài tại đỉnh \(D\) là:  \(360^\circ  - \left( {65^\circ  + 100^\circ  + 60^\circ } \right) = 135^\circ \)

Xét hình tứ giác ABCD có:

\(A+B+C+D=360^0\) (đ/l.....)

=>\(D=360^0-\left(A+B+C\right)=360^0-\left(65^0+117^0+71^0\right)=107^0\)

=>số đo góc ngoài ở đỉnh D là : 180⁰-107⁰=73⁰

Xét hình tứ giác ABCD :

=>107⁰

=>số đo góc ngoài ở đỉnh D là : 180⁰-107⁰=73⁰

Số đo góc ngoài tại đỉnh B là:

\(180^0-360^0+57^0+110^0+75^0=62^0\)

Tổng số đo các góc ngoài đỉnh B,C,D là 260 độ

mik đang cần gáp bài này mn giúp mik với

Số đo góc ngoài đỉnh C là:

\(180^0-71^0=109^0\)

Ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{0}\)(Định lí tổng các góc trong tứ giác)

\(\Rightarrow\)\(\widehat{D}=360^{0}-(\widehat{A}+\widehat{B}+\widehat{C})\)

\(=360^{0}-(65^{0}+117^{0}+71^{0}) =107^{0}\)

Gọi \(\widehat{D_{1}}\) là góc ngoài tại đỉnh D của tứ giác ABCD. Ta có:

\(\widehat{D}+\widehat{D_{1}}=180^{0}\) (\(\widehat{D}\) và \(\widehat{D_{1}}\) là hai góc kề bù)

\(\Rightarrow\) \(\widehat{D_{1}}=180^{0}-\widehat{D}\)

\(=180^{0}-107^{0}=73^{0}\)

Vậy số đo góc ngoài tại đỉnh D của tứ giác ABCD là 73⁰

Tứ giác ABCD có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

\(65^o+117^o+71^o+\widehat{D}=360^o\)

\(253^o+\widehat{D}=360^o\)

\(\widehat{D}=360^o-253^o=107^o\)

\(\Rightarrow\) Góc ngoài của \(\widehat{D}=180^o-107^o=73^o\)

Vậy số đo góc ngoài tại đỉnh D là \(73^o\)

Chọn C

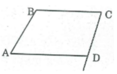
Trong tứ giác ABCD, ta có:

∠ A +  ∠ B +  ∠ C +  ∠ D =  360 0  (tổng các góc của tứ giác)

⇒  ∠ D =  360 0  – ( ∠ A +  ∠ B +  ∠ C )

=  360 0  – ( 65 0  +  117 0  +  71 0 ) =  107 0

∠ D + ∠ D 1  = 180 0  (2 góc kề bù) ⇒  ∠ D 1  =  180 0  -  ∠ D =  180 0  –  107 0  = 73o