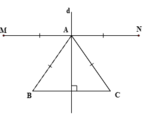
Cho tam giác ABC , AB=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, lấy điểm M sao co góc BAM = B và ÂM = AB . Trên nửa mặt phẳng bờ AC không chứa B , lấy điểm N sao cho góc CAN = C và AN=AC . Từ A vẽ d vuông góc . Chứng tỏ d là trung trực của MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN

Ta có hình vẽ:
Ta có:
góc MAB = góc ABC mà MAB và ABC ở vị trí so le trong => AM // BC (1)
góc NAC = góc ACB mà NAC và ACB ở vị trí so le trong => AN // BC (2)
Từ (1) và (2) mà theo tiên đề Ơ-clit qua 1 điểm nằm ngoài 1 đường thẳng chỉ kẻ được đúng 1 đường thẳng song song với đường thẳng ban đầu => MA trùng với NA hay 3 điểm A, M, N thẳng hàng
=> MN // BC
Mà d vuông góc với BC, MN // BC => MN vuông góc với d (quan hệ từ vuông góc -> song song) (2)
Mặt khác, AM = AB, AB = AC, AC = AN
=> AM = AN hay A là trung điểm của MN (3)
Từ (2) và (3) => d là đường trung trực của MN (đpcm)

bạn vào: http://olm.vn/hoi-dap/tim-kiem-google?q=%20Cho%20tam%20gi%C3%A1c%20ABC%20c%C3%B3%20AB%20AC.Tr%C3%AAn%20n%E1%BB%ADa%20m%E1%BA%B7t%20ph%E1%BA%B3ng%20b%E1%BB%9D%20AB%20kh%C3%B4ng%20ch%E1%BB%A9a%20C%20l%E1%BA%A5y%20%C4%91i%E1%BB%83m%20M%20sao%20cho%20g%C3%B3c%20BAM%20g%C3%B3c%20B%20v%C3%A0%20AM%20AB.Tr%C3%AAn%20n%E1%BB%ADa%20m%E1%BA%B7t%20ph%E1%BA%B3ng%20b%E1%BB%9D%20AC%20kh%C3%B4ng%20ch%E1%BB%A9a%20B%20l%E1%BA%A5y%20%C4%91i%E1%BB%83m%20N%20sao%20c

a) Xét tam giác vuông ABM và tam giác vuông NCA có:
NC=AB( gt)
CA=BM ( gt)
=> Tam giác ABM = Tam giác NCA
b) Xét tam giác vuông NCA và tam giác vuông BAC có:
AC chung
NC=BA
=> Tam giác NCA =Tam giác BAC
=> ^NAC =^BCA
mà hai góc trên ở vị trí so le trong
=> NA//BC (1)
c) Xét tam giác vuông ABC và tam giác vuông BMA có:
AB chung
AC=BM
=> Tam giác vuông ABC = Tam giác vuông BMA
=> ^MAB=^ABC
mà hai góc trên ở vị trí so le trong
=> MA//CB (2)
từ (1) , (2) => N, A, M thẳng hàng
Ta lại có: NA=AM ( Tam giác ABM =tam giác NCA)
=> A là trung điểm MN