Đổi 30 phút = 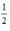 giờ.

Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0). Thời gian xe đi từ A đến B là 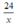 (giờ).

Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là 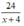 (giờ)

Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:

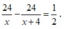
Giải phương trình:

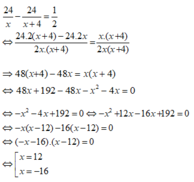
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.

Chọn đáp án A

Gọi vận tốc xe đạp khi đi từ A đến B là x (km/h) ( x>0)

\(\rightarrow\)Thời gian xe đạp đi từ A đến B là : \(\dfrac{48}{x}\) (giờ)

Vận tốc khi đi từ B đến A là x + 4 (km/h)

\(\rightarrow\)Thời gian xe đạp đi từ B đến A là : \(\dfrac{48}{x+4}\) (giờ)

Theo bài ra ta có : \(\dfrac{48}{x}-\dfrac{48}{x+4}=1\)

\(\rightarrow\) x = 12 (TMĐK:x>0)

Vậy vận tốc xe đạp khi đi từ A đến B là 12km/h

12

gọi x là vận tốc của xe đạp đi từ A->B; thời gian đi từ A->B là 24/x

x+4 là vận tốc đi từ B->A;  thời gian đi từ B->A là 24/(x+4)

vì thời gian về ít hơn thời gian đi 30' nên ta có ft

24/x - 24/(x+4)=1/2 <->(24x+96-24x)/(x²+4x)=1/2 <->96.2=x²+4x <-> x²+4x-192=0 <->(x²+4x+4)-196=0         <->(x+2)² -14² =0 <-> (x+2-14)(x+2+14)=0 <-> (x-12)(x+16)=0 <-> x=12(nhận) ;x=-16(loại)

vậy vận tốc của xe đạp đi từ A->B là 12km/h

Gọi x(km/h ) là vận tốc xe đạp đi từ a đến b (x>0)

do thời gian về ít hơn thời gian đi là 30p =1/2h . ta có pt:

\(\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}\)

\(\Leftrightarrow48\left(x+4\right)-48x=x\left(x+4\right)\)

\(\Leftrightarrow48x+192-48x=x^2+4x\)

\(\Leftrightarrow x^2+4x-192=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=12\\x=-16\left(ktm\right)\end{cases}}\)

Vậy vận tóc xe đạp đi từ a đến b là 12 km/h.

Đổi 30 phút = \(\frac{1}{2}\) giờ

Gọi vận tốc xe đạp đi từ A đến B là x ( x > 0 )

Tgời gian người đó đi từ A đến B là \(\frac{24}{x}\)

Thời gian người đó đi từ B đến A là \(\frac{24}{x+4}\left(h\right)\)

Theo đề, ta có phương trình :

\(\frac{24}{x}-\frac{24}{x+4}=12\)

\(\Leftrightarrow x1=12\left(n\right)\)

\(x2=-16\left(l\right)\)

Vậy vận tốc của xe đạp khi đi từ A đến B là 12 km/h

30 phút = \(\dfrac{1}{2}\)h.

Gọi vận tốc xe đạp đi từ A đến B là x (km/h, x>0)

Thời gian người đó đi từ A đến B là \(\dfrac{24}{x}\) (h)

Thời gian người đó đi từ B về A là \(\dfrac{24}{x+4}\) (h)

Theo đề, ta có pt : \(\dfrac{24}{x}-\dfrac{24}{x+4}=\dfrac{1}{2}\)

=> PT có 2 nghiệm \(x_1=12\left(nhận\right);x_2=-16\left(loại\right)\)

Vậy vận tốc của xe đạp khi đi từ A đến B là 12km/h.

Gọi x là quãng đường AB(x>0, km)

Ta có vận tốc lúc về là: 40+5=45(km/h)

Đổi 15'=1/4 h

Vì lúc về ít hơn lúc đi là 1/4 h, ta có pt:

\(\dfrac{x}{14}-\dfrac{1}{4}=\dfrac{x}{45}\)

\(\dfrac{9x}{360}-\dfrac{90}{360}=\dfrac{8x}{360}\)

\(9x-8x=90\)

\(x=90\)

Vậy: Độ dài quãng đường AB là 90km