Ta có:\(x+y=1\)\(\Rightarrow x=1-y\)

Khi đó: \(P=\left(1-y\right)^3+y^3+\left(1-y\right)y\)

               \(=1-3y+3y^2-y^3+y^3+y-y^2\)

                \(=2y^2-2y+1\)

                 \(=2\left(y^2-y+\frac{1}{4}\right)-\frac{1}{2}+1\)

                  \(=2\left(y-\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\)

Dấu ''='' xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)

cậu thế vào, Ta có:

x=12,y=5

Vậy x+y=17.Toán vòng 11 olympic chứ gì, mình thi rồi.

5 và 12 bạn nhé 

1) Giả sử: \(9x+5=n\left(n+1\right)\left(n\in Z\right)\)

\(36x+20-4n^2+4n\)

\(\Rightarrow36x+21=4n^2+4n+1\)

\(\Rightarrow3\left(12x+7\right)=\left(2n+1\right)^2\)

\(\left(2n+1\right)^2\)là số chính phương nên sẽ chia hết cho 3 => (2n+1)² chia hết cho 9

Lại có: 12x+7 ko chia hết cho 3 => 3(12x+7) ko chia hết cho 9

Chứng tỏ không tồn tại số nguyên x nào để 9x+5=n(n+1)

2) Ta có: xy + 3x - y = 6 =>x(y+3) - y = 6 

=>x(y+3) - y - 3 = 3 =>x(y+3) - (y+3) = 3

=> (y+3)(x-1) =3

Vì x, y là các số nguyên nên y+3;x-1 là các số nguyên

Ta có bảng sau:

Câu 2:

\(A-4=2x+3y\Rightarrow\left(A-4\right)^2=\left(2x+3y\right)^2\)

\(\left(A-4\right)^2\le\left(2^2+3^2\right)\left(x^2+y^2\right)=676\)

\(\Rightarrow-26\le A-4\le26\)

\(\Rightarrow-22\le A\le30\)

\(A_{max}=30\) khi \(\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)

\(A_{min}=-22\) khi \(\left\{{}\begin{matrix}x=-4\\y=-6\end{matrix}\right.\)

\(2x+3y=1\Rightarrow y=\frac{1-2x}{3}\)

Do \(x;y\ge0\Rightarrow0\le x\le\frac{1}{2}\)

\(A=x^2+3\left(\frac{1-2x}{3}\right)^2=x^2+\frac{1}{3}\left(4x^2-4x+1\right)=\frac{7}{3}x^2-\frac{4}{3}x+\frac{1}{3}\)

\(A=\frac{7}{3}\left(x-\frac{2}{7}\right)^2+\frac{1}{7}\ge\frac{1}{7}\)

\(\Rightarrow A_{min}=\frac{1}{7}\) khi \(x=\frac{2}{7};y=\frac{1}{7}\)

Mặt khác \(A=\frac{1}{3}x\left(7x-4\right)+\frac{1}{3}\)

Do \(x\le\frac{1}{2}\Rightarrow7x-4< 0\Rightarrow x\left(7x-4\right)\le0\)

\(\Rightarrow A\le\frac{1}{3}\Rightarrow A_{max}=\frac{1}{3}\) khi \(x=0;y=\frac{1}{3}\)

Vì

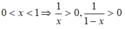
Áp dụng bất đẳng thức Cô – si đối với hai số 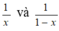 ta được:

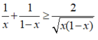
Vì 0 < x < 1 ⇒ 1 - x > 0

Áp dụng bất đẳng thức Cô – si đối với hai số 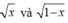 ta được:

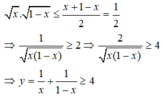
Dấu “ = ” xảy khi và chỉ khi

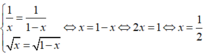
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2