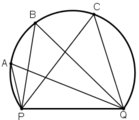
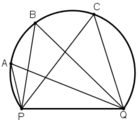
Một cầu thủ đang đứng ở vị trí A để sút bóng vào khung thành BC. Tính đường kính của đường tròn đi qua ba điểm A,B,C. Biết góc sút BAC là 68° và chiều rộng của BC là 5m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì trong hình vẽ mặt sân được vẽ nghiêng nên nếu đo trực tiếp trong sách giáo khoa sẽ không đúng bằng góc thực tế.
Vẽ một tam giác bằng dụng cụ học tập trên giấy có một góc đúng bằng góc sút. Từ đó sử dụng dụng cụ học tập là thước đo góc để đo góc sút.

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .

Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .


Áp dụng định lý sin cho tam giác ABC, ta có:
\(2R_{giếng}=\dfrac{BC}{\sin A}=\dfrac{5}{\sin145^o}\) \(\Rightarrow R_{giếng}=\dfrac{5}{2\sin145^o}\) (m)
\(\Rightarrow S_{giếng}=\pi R_{giếng}^2=\pi\left(\dfrac{5}{2\sin145^o}\right)^2\approx59,68\left(m^2\right)\)

Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
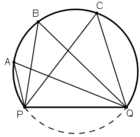
Các góc 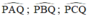 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 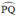
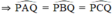
Kiến thức áp dụng
+ Trong cùng một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
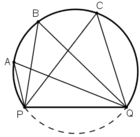
Các góc 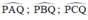 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 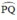
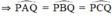

Chọn B.
Phương pháp
Tính xác suất theo phương pháp biến cố đối: “Không có cầu thủ nào sút vào”.
Cách giải:
Gọi A là biến cố: “Ít nhất một cầu thủ sút vào”.
Khi đó A ¯ là biến cố: “Không có cầu thủ nào sút vào”.