Bài 7: Cho tam giác DEF cân tại D, DI là phân giác của EDF (I thuộc EF). Gọi N là trung điểm của
IF. Vẽ điểm M sao cho N là trung điểm của DM. Chứng minh rằng:
1) ADIN = AMFN và MF 1 EF.
2) Cho DE = 8cm, EF = 12cm. Tính độ dài đoạn thẳng FM.
3) DF > MF và IDN > NDF.
4) Gọi K là trung điểm của ME. Chứng minh D, I, K thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ý C là ghi sai đề bài rồi nhé
Còn ý d khó nhất thì giải như sau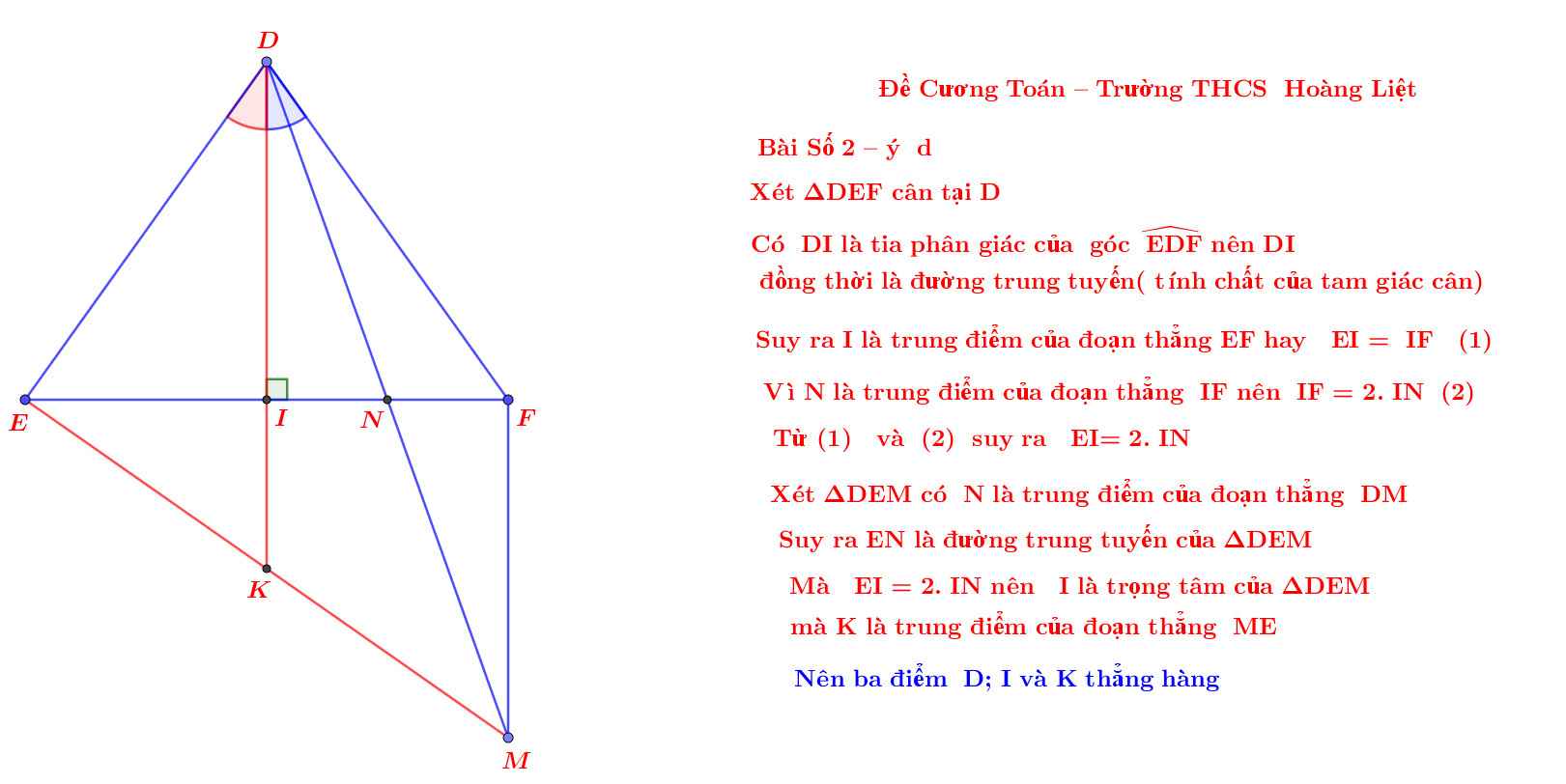

Cho tam giác ABC vuông tại A.Gọi M là trung điểm của BC.Trên tia đối của tia MA lấy điểm E sao cho MA=ME.

tam giác DEF cân tại D suy ra DE=DF, góc DEF = góc DFE
Xét tam giác KEF và tam giác HFE
có EF chung
góc EKF=góc EHF = 900
góc KEF=góc HFE (CMT)
suy ra tam giác KEF và tam giác HFE (cạnh huyền-góc nhọn)
suy ra EK = HF
mà DK+KE=DE, DH+HF=DF
lại có DE=DF (CMT)
suy ra KD=DH
b) xét tam giác DKO và tam giác DHO
có DO chung
góc DKO = góc DHO = 900
DK = DH (CMT)
suy ra tam giác DKO = tam giác DHO ( cạnh huyền-cạnh góc vuông)
suy ra góc KDO = góc HDO
suy ra DO là tia phân giác của góc EDF (1)
c) Vì DK = DH suy ra tam giác DKH cân tại D
suy ra góc DKH= góc DHK
suy ra góc DKH+ góc DHK + góc KDH = 1800
suy ra góc DKH=(1800 - góc KDH) :2 (2)
Tam giác DEF cân tại D
suy ra góc DEF + góc DFE + góc EDF = 1800
suy ra góc DEF = (1800 - góc KDH) :2 (3)
Từ (2) và (3) suy ra góc DKH = góc DEF
mà góc DKH đồng vị với góc DEF
suy ra KH // EF
d) Xét tam giác DEI và tam giác DFI
có DE = DF (CMT)
DI chung
EI = IF
suy ra tam giác DEI = tam giác DFI (c.c.c)
suy ra góc EDI = góc FDI
suy ra DI là tia phân giác của góc EDF (4)
Từ (1) và (4) suy ra DO trùng DI
hay ba điểm D, O, I thẳng hàng.

a: Ta có: ΔDEF cân tại D
mà DI là đường trung tuyến
nên DI là phân giác
b: Xét ΔDMI vuông tại M và ΔDNI vuông tại N có
DI chung
\(\widehat{MDI}=\widehat{NDI}\)
DO đó; ΔDMI=ΔDNI
Suy ra: IM=IN
hay ΔIMN cân tại I

a) xét tam giác DHE và tam giác DHF có
DH chung
DE = DF (gt)
góc DHE = góc DHF (=90 độ)
=> tam giác DHE = tam giác DHF (c.g.c)
=> HE = HF
=> H là trung điểm của EF
b) xét tam giác EMH và tam giác FNH có
HE = HF (cmt)
Góc MEH = góc MFH (gt)
Góc EHM = góc FHM (đối đỉnh)
=> tam giác EMH = tam giác FNH (g.c.g)
=> HM = HN
=> tam giác HMN cân tại H
a: Xét ΔDEH vuông tại H và ΔDFH vuông tại H có
DE=DF
DH chung
=>ΔDEH=ΔDFH
=>EH=FH
=>H là trung điểm của EF
b: Xet ΔDMH và ΔDNH có
DM=DN
góc MDH=góc NDH
DH chung
=>ΔDMH=ΔDNH
=>HM=NH
c: Xet ΔDEF có DM/DE=DN/DF
nên MN//EF
d: ΔDMN cân tại D
mà DI là trug tuyến
nên DI là phân giác của góc EDF
=>D,I,H thẳng hàng

1: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HE=HF
EF=8cm
nên HE=4cm
=>DH=3cm
2: Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
Suy ra: EM=FN
3: Xét ΔNEF và ΔMFE có
NE=MF
\(\widehat{NEF}=\widehat{MFE}\)
FE chung
Do đó:ΔNEF=ΔMFE
Suy ra: \(\widehat{KFE}=\widehat{KEF}\)
=>ΔKEF cân tại K
hay KE=KF
4: Ta có: DE=DF
nên D nằm trên đường trung trực của EF(1)
ta có: KE=KF
nên K nằm trên đường trung trực của EF(2)
ta có: HE=HF
nên H nằm trên đường trung trực của EF(3)
Từ (1), (2) và (3) suy ra D,K,H thẳng hàng

các bạn giúp mik với
1: Xét ΔDIN và ΔMFN có
ND=NM
\(\widehat{DNM}=\widehat{MNF}\)
NI=NF
Do đó: ΔDIN=ΔMFN
Suy ra: DI=FM
mà DI<DF
nên FM<DF
2: EF=12cm nên IF=6cm
\(\Leftrightarrow DI=FM=\sqrt{8^2-6^2}=2\sqrt{7}\left(cm\right)\)