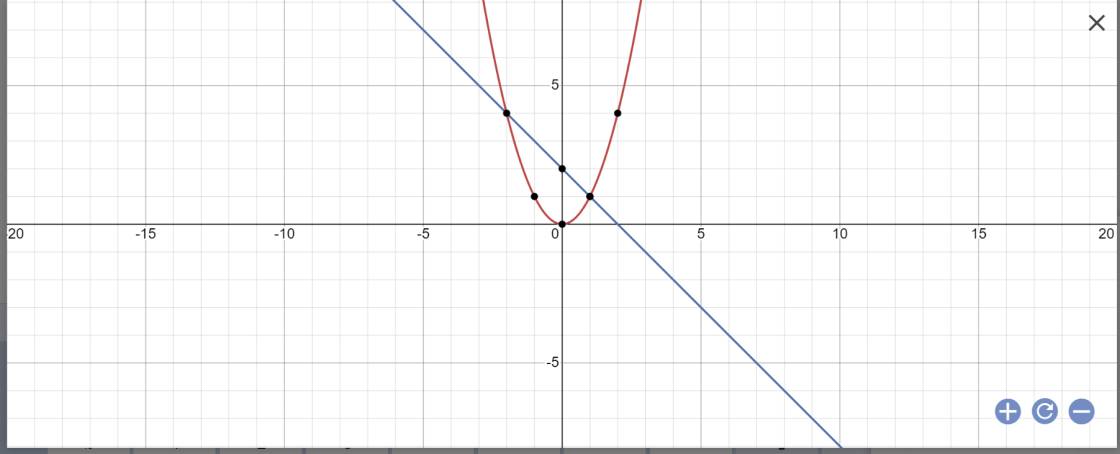
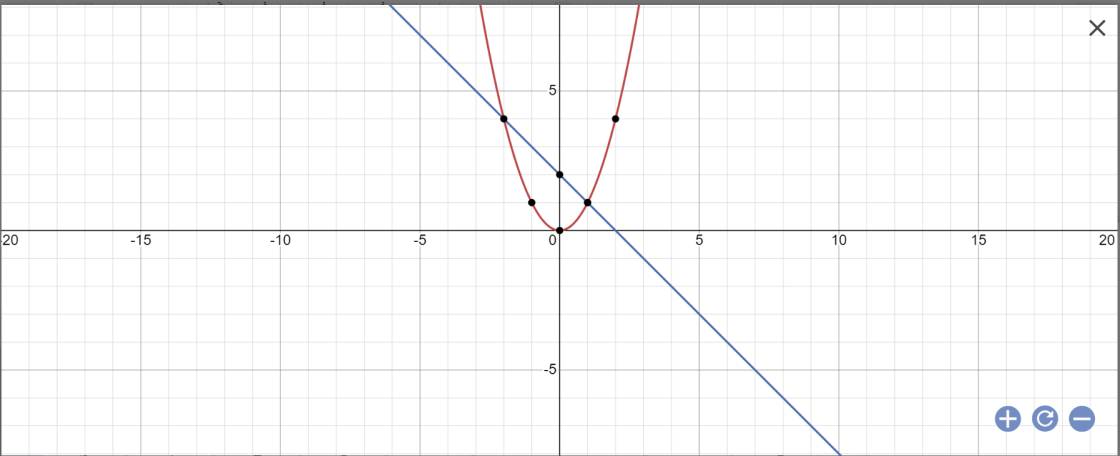
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = - x2
a) Vẽ parabol (P)
b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y = - x – 2 và (P).
c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại M
Bài 2 Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
CMR: (d) luôn cắt (P) tại 2 điểm phân biệt
a) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P = ![]() khi m thay đổi
khi m thay đổi
Bài 3. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt nằm bên phải trục tung
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1
Tìm m sao cho (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho ![]()
Bài 6. Cho parabol (P) : y = ![]() x2 và đường thẳng (d) : y = mx -
x2 và đường thẳng (d) : y = mx - ![]() m2 + m +1.
m2 + m +1.
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho ![]() .
.