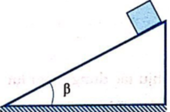
Một vật trượt không vận tốc đầu từ đỉnh mặt phẳng nghiêng cao 1,25m. Cho gia tốc
rơi tự do g = 10m/s2.
a) Vật trượt không ma sát trên mặt phẳng nghiêng. Hãy tính vận tốc của vật tại chân mặt phẳng nghiêng.
b) Khi đến chân mặt phẳng nghiêng, vật tiếp tục trượt trên mặt phẳng nằm ngang nối liền với mặt phẳng
nghiêng. Thời gian chuyển động của vật trên mặt phẳng ngang là 5s. Tính hệ số ma sát giữa vật và mặt phẳng ngang.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

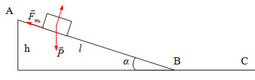
Ta có:
+ Cơ năng tại A:
\(W_A=mgh=1.9,8.1=9,8\left(J\right)\)
+ Trong khi vật chuyển động từ A đến B , tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát.
Áp dụng đl bảo toàn chuyển hóa năng lượng , ta có:
\(W_A=W_{db}-A_{Fms}\left(1\right)\)
Chọn chiều dương trùng chiều chuyển động của vật , ta có:
+ Động năng tại B : \(W_{dg}=\dfrac{1}{2}mv^2_B\)
+ Công của lực ma sát:
\(A=F_{ms}.s.cos\beta=-F_{ms}.l=-\mu P.sin\alpha.l\)
Thay vào (1) ta được:
\(W_A=W_{dB}+\left|A_{Fms}\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B+\left|-\mu.P.sin\alpha.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}mv^2_B\left|-\mu mg.\dfrac{h}{l}.l\right|\)
\(\Leftrightarrow9,8=\dfrac{1}{2}1.v^2_B+\left|-0,05.1.9,8.\dfrac{1}{10}.10\right|\)
\(\Rightarrow v^2_B=18,62\)
\(\Rightarrow v_B\approx4,32m/s\)

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)


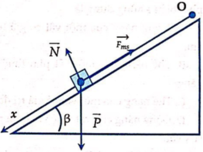
- Khi vật trượt trên mặt phẳng nghiêng, có 3 lực tác dụng lên vật:
+ Trọng lực: P →
+ Phản lực của mặt phẳng nghiêng: N → (có phương vuông góc với mp nghiêng) (trong hình kí hiệu là Q → )
+ Lực ma sát trượt: F → m s t
- Theo định luật II Niutơn:
P → + N → + F → m s t = m a →
Mà: P → = P → 1 + P → 2
Nên: P → 1 + P → 2 + F → m s t + N → = m a →
Mặt khác: P → 2 + N → = 0 →
- Chọn chiều dương là chiều chuyển động của vật:
− F m s t + P 1 = m a ⇒ − μ t N + P sin α = m a
Với: N = P 2 = P c o s α = m g c o s α
Với: sin α = B C A C = 5 10 = 1 2 c o s α = A B A C = A C 2 − B C 2 A C = 10 2 − 5 2 10 = 3 2
a = g ( sin α − μ t c o s α ) = 9 , 8 ( 0 , 5 − 0 , 1. 3 2 ) = 4 , 05 m / s 2
Đáp án: C


![]()
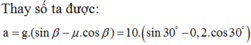
![]()
+ Theo công thức liên hệ a;v; S trong chuyển động thẳng biến đổi đều ta có:
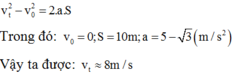

Chọn mốc thế năng tại B ( Hình 93).
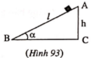
Chuyển động không có ma sát nên: W A = W B
Cơ năng tại A: ![]()
Cơ năng tại B: ![]()
Suy ra
![]()