Hỗn hợp X gồm H2, CnH2n và CnH2n – 2 (hai hiđrocacbon đều mạch hở, n là số nguyên tử cacbon) có tỉ khối hơi so với H2 là 7,8. Cho hỗn hợp X qua xúc tác Ni nung nóng để các phảnứng xảy ra hoàn toàn, thu được hỗn hợp Y có tỉ khối so với hỗn hợp X là 20/9 a) Viết phương trình phản ứng. b) Xác định công thức phân tử, công thức cấu tạo của hai hiđrocacbon và tính phần trăm thể tích của mỗi chất trong hỗn hợp X.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Gọi CTPT của X là CnH2n-2 : a (mol) ; nH2 = b (mol)
Mtrước = 4,8.2 = 9,6 (g/mol) ; Msau = 8.2 = 16 (g/mol).
Phản ứng xảy ra hoàn toàn, Msau= 16 (g/mol) nên trong hỗn hợp sau có H2 => CnH2n-2 phản ứng hết
CnH2n-2 + 2H2 → CnH2n+2
a → 2a → a (mol)
=> nsau = nH2 dư + nCnH2n+2 = ( b- 2a) + a
=> nsau = b - a
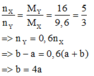
Ta có: mCnH2n-2 + mH2 = mX
=> (14n – 2)a + 2b = 9,6. ( a+b)
=> (14n -2)a + 8a = 9,6. (a + 4a)
=> n = 3 => C3H4
![]()

Chọn đáp án B
Gọi CTPT của X là CnH2n-2 : a (mol) ; nH2 = b (mol)
Mtrước = 4,8.2 = 9,6 (g/mol) ; Msau = 8.2 = 16 (g/mol).
Phản ứng xảy ra hoàn toàn, Msau= 16 (g/mol) nên trong hỗn hợp sau có H2 => CnH2n-2 phản ứng hết
CnH2n-2 + 2H2 → CnH2n+2
a → 2a → a (mol)
=> nsau = nH2 dư + nCnH2n+2 = ( b- 2a) + a
=> nsau = b - a
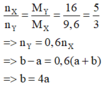
Ta có: mCnH2n-2 + mH2 = mX
=> (14n – 2)a + 2b = 9,6. ( a+b)
=> (14n -2)a + 8a = 9,6. (a + 4a)
=> n = 3 => C3H4
![]()

Đáp án D
Điều kiện : 1 ≤ n ≤ 4 ; 2 ≤ m ≤ 4 1 ≤ n + m ≤ 4 ⇒ n = 1 m = 2
=> Công thức của các hidrocacbon là CH4, C2H4 và C4H4
Gọi x, y, z lần lượt là sốm ol của CH4, C2H4 và C4H4 có trong hỗn hợp X.
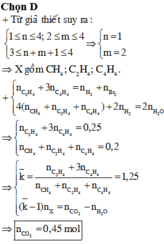
Theo bảo toàn liên kết π, ta có :
∑ l k π = y + 3 z = n H 2 + n B r 2 =0,1+0,15=0,25 (1)
Theo bảo toàn nguyên tố C, H:
nH2O = 2nCH4 + 2nC2H4 + 2nC4H4 + nH2 = 2(x+y+z) = 0,4
=> x +y + z = 0,2 (2)
(1) (2) => x + 2y + 4z = 0,45 = a = nCO2

Đáp án D
Theo định luật bảo toàn khối lượng
mX=mY=>nX.MX=nY.MY ⇔ 2.4,7.4 =nY.9,4.4 ó nY= 1.
nX - nY = n H2 phản ứrng = nancol sinh ra
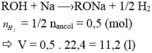



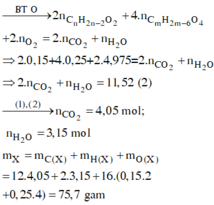
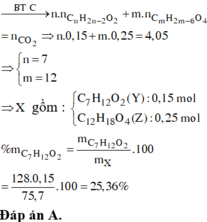
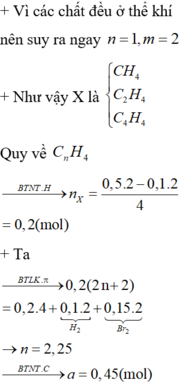
a)
CnH2n-2 + H2 --to,Ni--> CnH2n
CnH2n + H2 --to,Ni--> CnH2n+2
CnH2n-2 + 2H2 --to,Ni--> CnH2n+2
b)
Có: mX = mY (Theo ĐLBTKL)
\(d_{Y/X}=\dfrac{M_Y}{M_X}=\dfrac{\dfrac{m_Y}{n_Y}}{\dfrac{m_X}{n_X}}=\dfrac{20}{9}\)
=> \(\dfrac{n_X}{n_Y}=\dfrac{20}{9}\)
Giả sử nX = 20(mol); nY = 9(mol)
nH2(pư) = 20 - 9 = 11 (mol)
\(m_X=7,8.2.20=312\left(g\right)\)
Gọi \(\left\{{}\begin{matrix}n_{H_2}=a\left(a\ge11\right)\\n_{C_nH_n}=b\left(mol\right)\\n_{C_nH_{2n-2}}=c\left(mol\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a+b+c=20\left(1\right)\\2a+14bn+14cn-2c=312\left(2\right)\end{matrix}\right.\)
- Nếu H2 phản ứng hết => a = 11
=> \(\left\{{}\begin{matrix}b+c=9\\14bn+14cn-2c=290\end{matrix}\right.\)
=> 126n = 290 + 2c
Mà c > 0 => n > 2,3
c < 9 => n < 2,4
=> 2,3 < n < 2,4 (vô lí)
=> H2 dư
* Sơ đồ:
\(X\left\{{}\begin{matrix}H_2:a\left(mol\right)\\C_nH_{2n}:b\left(mol\right)\\C_nH_{2n-2}:c\left(mol\right)\end{matrix}\right.\underrightarrow{t^o,Ni}Y\left\{{}\begin{matrix}H_2:a-11\left(mol\right)\\C_nH_{2n+2}:b+c\left(mol\right)\end{matrix}\right.\)
Bảo toàn H: 2a + 2bn + 2cn - 2c = 2a - 22 + 2bn + 2b + 2cn + 2c
=> 2b + 4c = 22
=> b + 2c = 11 (3)
Lấy (1) - (3) => a - c = 9
=> 2a - 2c = 18
Thay vào (2):
14bn + 14cn = 294
=> bn + cn = 21
=> \(n\left(b+c\right)=21\)
=> \(n\left(b+\dfrac{11-b}{2}\right)=21\)
=> \(n.\dfrac{11+b}{2}=21\)
=> \(n=\dfrac{42}{11+b}\)
Mà b > 0 => n < 3,8
b < 11 => n > 1,9
=> 1,9 < n < 3,8
=> n = 2 hoặc n = 3
TH1: n = 2
Có: \(\left\{{}\begin{matrix}b+2c=11\\2b+2c=21\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}b=10\\c=0,5\end{matrix}\right.\)
=> a = 9,5 (mol) => Loại do a \(\ge11\)
TH2: n = 3
Có: \(\left\{{}\begin{matrix}b+2c=11\\3b+3c=21\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}b=3\\c=4\end{matrix}\right.\)
=> a = 13 (Thỏa mãn)
Vậy CnH2n, CnH2n-2 lần lượt là C3H6, C3H4
CTCT:
C3H6: \(CH_2=CH-CH_3\)
C3H4: \(CH\equiv C-CH_3\)
X\(\left\{{}\begin{matrix}\%V_{H_2}=\dfrac{13}{20}.100\%=65\%\\\%V_{C_3H_6}=\dfrac{3}{20}.100\%=15\%\\\%V_{C_3H_4}=\dfrac{4}{20}.100\%=20\%\end{matrix}\right.\)