cho ∆ABC Với đường trug tuyến AD, Tia phân giác của góc ADB cắt cạnh AB ở E , tia phân giác góc ADC cắt cạnh AC tại M. a) Chứng minh AE/EB =AD/BD . b) chứng minh AM,CD = AD,MC . c) chứng minh EM//BC. d) Gọi K là giao điểm của AD và EM . Chứng minh K là trung điểm của EM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


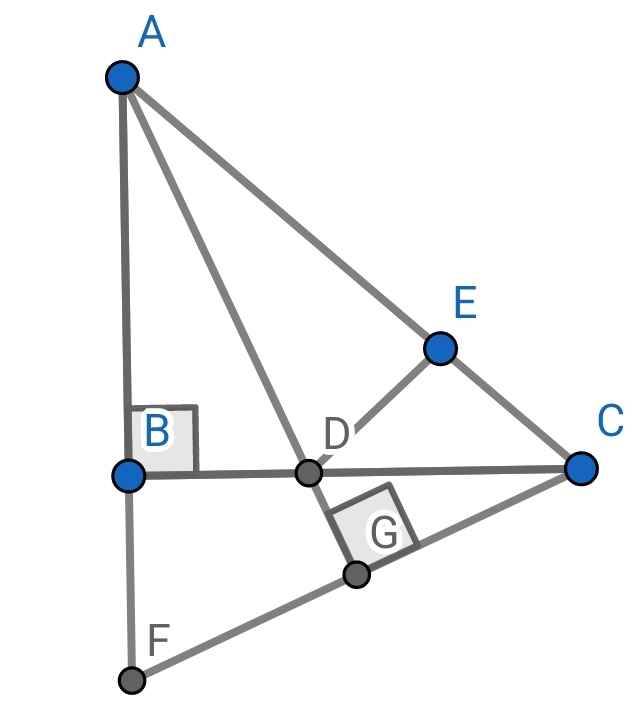
a) Xét ∆ADB và ∆ADE có:
AD chung
Góc BAD = góc EAD (AD là tia phân giác của góc BAC)
AB = AE (gt)
⇒∆ADB = ∆ADE (c-g-c)
b) Do ∆ADB = ∆ADE (c-g-c)
⇒góc ABD = góc AED (hai góc tương ứng)
⇒góc AED = 90⁰
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do góc BAD = góc EAD (cmt)
⇒góc FAG = góc CAG
Xét hai tam giác vuông: ∆AGF và ∆AGC có:
AG chung
góc FAG = góc CAG (cmt)
⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)
⇒AF = AC (hai cạnh tương ứng)
Mà AF = AB + BF
AC = AE + EC
AB = AE
⇒BF = CE

a) Xét tg ABM và ACM có :
AB=AC(gt)
AM-cạnh chung
MB=MB(gt)
=> Tg ABM=ACM(c.c.c)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
=> AM là tia pg góc A (đccm)
b) Xét tg BNC và DNC có :
BC=CD(gt)
\(\widehat{DCN}=\widehat{BCN}\left(gt\right)\)
NC-cạnh chung
=> Tg BNC=DNC(c.g.c)
\(\Rightarrow\widehat{CND}=\widehat{CNB}=\frac{\widehat{DNB}}{2}=\frac{180^o}{2}=90^o\)
\(\Rightarrow CN\perp BD\left(đccm\right)\)
c) Có : AB=AC(gt)
=> Tg ABC cân tịa A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(1)
- Do tg BNC=DNC(cmt)
\(\widehat{ABC}=\widehat{BDC}\)(2)
- Từ (1) và (2)\(\Rightarrow\widehat{BDC}=\widehat{ACB}\)
- Có : \(\widehat{ADC}+\widehat{BDC}=180^o\)
\(\widehat{ACB}+\widehat{BCE}=180^o\)
Mà : \(\widehat{BDC}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow\widehat{BCE}=\widehat{ADC}\left(đccm\right)\)
d) Xét tg ACD và EBC có :
BC=CD(gt)
DA=CE(gt)
\(\widehat{BCE}=\widehat{ADC}\left(cmt\right)\)
=> Tg ACD=EBC(c.g.c)
=> AC=BE
Mà AC=AB(gt)
=> BE=AB (đccm)
#H
