Tính sinC, cosC, CotgC nếu biết tgC = 0.75. Giúp mình với :)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


dung tinh chat : tanC.cotC=1=>cotC=4/3
sau đó dùng tính chất:\(1+cot^2C=\frac{1}{sin^2C}\Rightarrow sin^2C\)=0,36 =>sinC=0,6=>cosC=sinC / tanC=0,8

mình trả lời hơi muộn :(
1, Theo giả thiết ta có C = 45* nên tam giác ABC là tam giác vuông cân
Suy ra AB = AC = 2 (cm) Mà theo đánh giá của Pitago thì :BC^2 = 8 <=> BC = căn 8
Ta có hệ thức lượng sau : AB.AC=AH.BC <=> 4=căn 8 . AH<=> AH=2/căn2
Lại có hệ thức lượng sau : AC^2=CH.BC<=>4=căn 8 . CH <=> CH=2/căn2
Mặt khác : +)Cos alpha = AB/BC = 2/căn8 = 1/căn2
+)Cos beta = AC/BC = 2/căn8 = 1/căn2
+) Sin alpha = AC/BC = 2/căn8 = 1/căn2
+) Sin beta = AB/BC = 2/căn8 = 1/căn2
Vậy ...
Mấy câu còn lại để từ từ mình làm dần

cotC=1/tanC = 4/3
=>\(\frac{ac}{ab}=\frac{4}{3}\)=>ac=4k , ab=3k {với k \(\ge\) 0 }
=>BC = 5k
=>sinC =\(\frac{3}{5}\)
cosC=\(\frac{4}{5}\)
tick nha

a)\(VT=sinA+sinB+sinC=2sin\frac{A+B}{2}.cos\frac{A-B}{2}+2sin\frac{C}{2}.cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)=4cos\frac{C}{2}.cos\frac{A}{2}.cos\frac{B}{2}\)(đpcm)

\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)
\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)
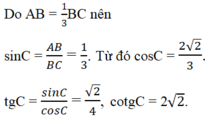
sinC=4/5
cosC= 3/5
CotgC= 3/4
Bạn có thể ghi lời giải cho mình được không vậy?