Để đo chiều dài của cây bàng (đoạn AB) người ta dùng một cái cọc MN cao 1,5m đặt vuông góc với mặt đất có gắn thước ngắm sao cho hướng đi qua A của cây và 3 điểm A, M, C thẳng hàng. Người ta đo được khoảng cách từ C đến N là 1,2 và từ C đến B là 6m. Tính chiều cao của cây.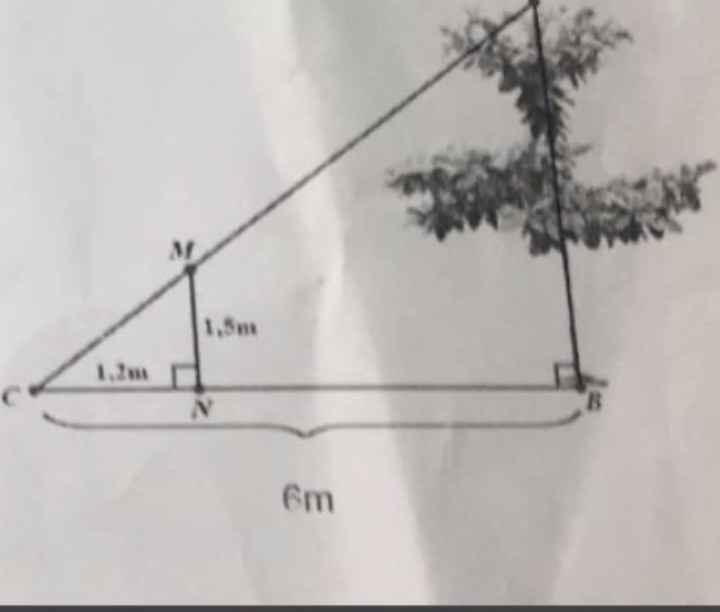
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

40 cm = 0,4 m .
Nếu cọc cao 1 m thì bóng của nó dài : 0,4 : 2 = 0,2 (m)
Vậy chiều cao của cây là : 3 : 0,2 = 15 (m)
Đáp số : 15 m

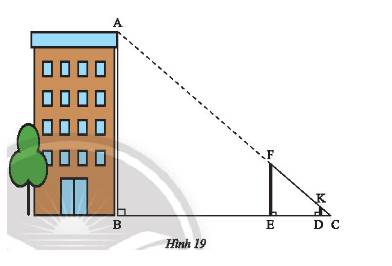
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.

Gọi chiều cai của xây là x(m) (x>0)
Áp dụng công thức
\(\frac{200}{50}\)=\(\frac{x}{400}\)
Từ đó tìm đk x=1600cm=16m(tmđk của x)
CHỌN A

Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
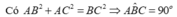
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)