Cho parabol (P): Y= -x2/4 và đường thẳng (d): y= -1/2x+m
Với m=-2 hãy vẽ (P) và (d) trên cùng một hệ trục tọa độ rồi tìm tọa độ các giao điểm của (P) và (D) bằng phép tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)

a,
| -4 | -2 | 0 | 2 | 4 | |
| \(y=\frac{1}{4}x^2\) | 4 | 1 | 0 | 1 | 4 |
| \(y=-\frac{1}{2}x+2\) | 4 | 3 | 2 | 1 | 0 |
Bạn tự vẽ ha.
b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
\(\frac{1}{4}x^2=-\frac{1}{2}x+2\)
\(\Leftrightarrow\frac{1}{4}x^2+\frac{1}{2}x-2=0\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=-4\\x=2\end{cases}}\)
\(x=-4\Rightarrow y=4\)
\(x=2\Rightarrow y=1\)
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)
Bạn tham khảo link này nha:
https://olm.vn/hoi-dap/detail/214561933532.html
Chúc bạn học tốt
Forever

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+x-2=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(x-1\right)=0\\y=-x+2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;4\right);\left(1;1\right)\right\}\)

b: Khi m=2 thì \(y=\left(2\cdot2-1\right)x-2^2+2=3x-2\)
Phương trình hoành độ giao điểm là:
\(x^2-3x+2=0\)
=>x=2 hoặc x=1
Khi x=2 thì y=4
Khi x=1 thì y=1
c: Phương trình hoành độ giao điểm là:
\(x^2-\left(2m-1\right)x+m^2-2=0\)
\(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2\right)\)
\(=4m^2-4m+1-4m^2+8=-4m+9\)
Để (P) cắt (d) tại hai điểm phân biệt thì -4m+9>0
=>-4m>-9
hay m<9/4

b,
Phương trình hoàng độ giao điểm của (p) và (d) là:
1
4
x
2
=
−
1
2
x
+
2
⇔
1
4
x
2
+
1
2
x
−
2
=
0
⇔
x
2
+
2
x
−
8
=
0
⇔
(
x
+
4
)
(
x
−
2
)
=
0
⇔
\orbr
{
x
=
−
4
x
=
2
x
=
−
4
⇒
y
=
4
x
=
2
⇒
y
=
1
Vậy tọa độ giao điểm của (p) và (d) là (-4;4) ; (2;1)

a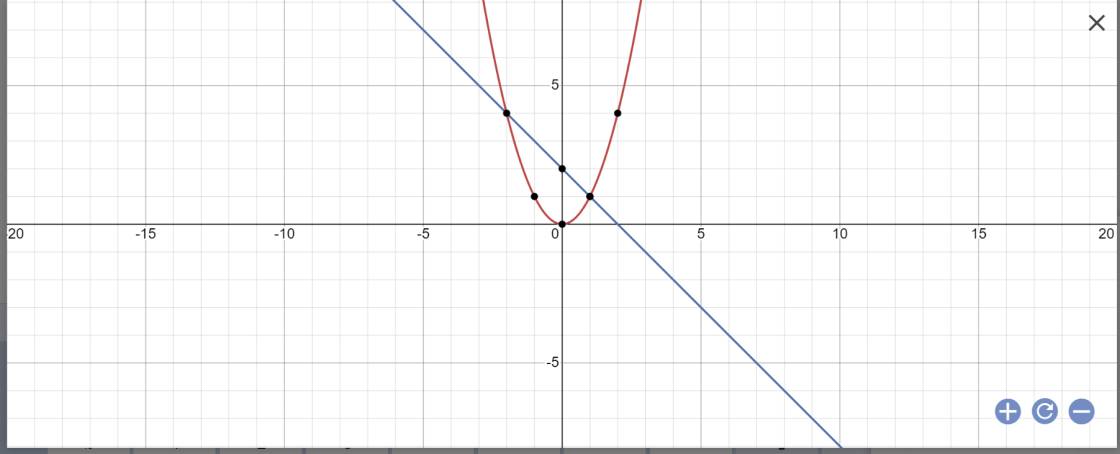
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a) Bạn tự vẽ
b) Phương trình hoành độ giao điểm của (P) và (d)
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
+) Với \(x=1\) thì \(y=1\)
+) Với \(x=-2\) thì \(y=4\)
Vậy (P) cắt (d) tại 2 điểm \(\left(1;1\right)\) và \(\left(-2;4\right)\)

1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
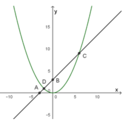
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .