Tim căn thức bậc 2 của 8+6i
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
![]()
![]()
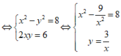
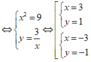
Do đó z có hai căn bậc hai là 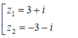

Chọn A.
Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.
Ta có:
![]()
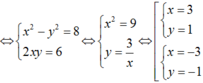
Do đó z có hai căn bậc hai là 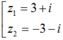

\(=\sqrt{5}-\sqrt{3}+\sqrt{5}-2=2\sqrt{5}-2-\sqrt{3}\)

a: ĐKXĐ: x-2>=0 và 6-2x>=0
=>2<=x<=3
b: DKXĐ: x+2>=0
=>x>=-2

Vì đây là lần đầu tiên bn gửi câu hỏi nên mk đã kiên nhẫn dịch cái đề và hi vọng nó đúng!
Ta có: \(\left(\sqrt{8+2\sqrt{7}}+2.\sqrt{8-2\sqrt{7}}\right).\left(\sqrt{63}+1\right)\)
\(=\left(\sqrt{7+2\sqrt{7}+1}+2.\sqrt{7-2\sqrt{7}+1}\right).\left(\sqrt{63}+1\right)\)
\(=\left(\sqrt{\left(\sqrt{7}+1\right)^2}+2.\sqrt{\left(\sqrt{7}-1\right)^2}\right)\left(\sqrt{63}+1\right)\)
\(=\left(\left|\sqrt{7}+1\right|+2.\left|\sqrt{7}-1\right|\right).\left(\sqrt{63}+1\right)\)
\(=\left(\sqrt{7}+1+2\sqrt{7}-2\right)\left(\sqrt{63}+1\right)\)
\(=\left(3\sqrt{7}-1\right)\left(\sqrt{63}+1\right)\)
\(=\left(\sqrt{63}-1\right)\left(\sqrt{63}+1\right)=63-1=62\)
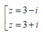
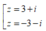

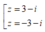

Đặt \(\sqrt{8+6i}=x+yi\) với \(x;y\in R\)
\(\Rightarrow8+6i=x^2+2xyi+y^2i^2=x^2-y^2+2xyi\)
\(\Rightarrow\left\{{}\begin{matrix}x^2-y^2=8\\xy=3\end{matrix}\right.\) \(\Rightarrow x^2-\dfrac{9}{x^2}=8\)
\(\Rightarrow x^4-8x^2-9=0\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=1\\x=-3\Rightarrow y=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{8+6i}=3+i\\\sqrt{8+6i}=-3-i\end{matrix}\right.\)