a) Cho trước 5 điểm M, N, P, Q, R trong đó chỉ có 3 điểm P, Q, R thẳng hàng ngoài ra không
còn ba điểm nào thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu
đường thẳng là những đường thẳng nào?
b) Cho trước 9 điểm trong đó có đúng 5 điểm thẳng hàng ngoài ra không còn ba điểm nào
thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng?
Mn giúp em với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
11 tháng 9 2018
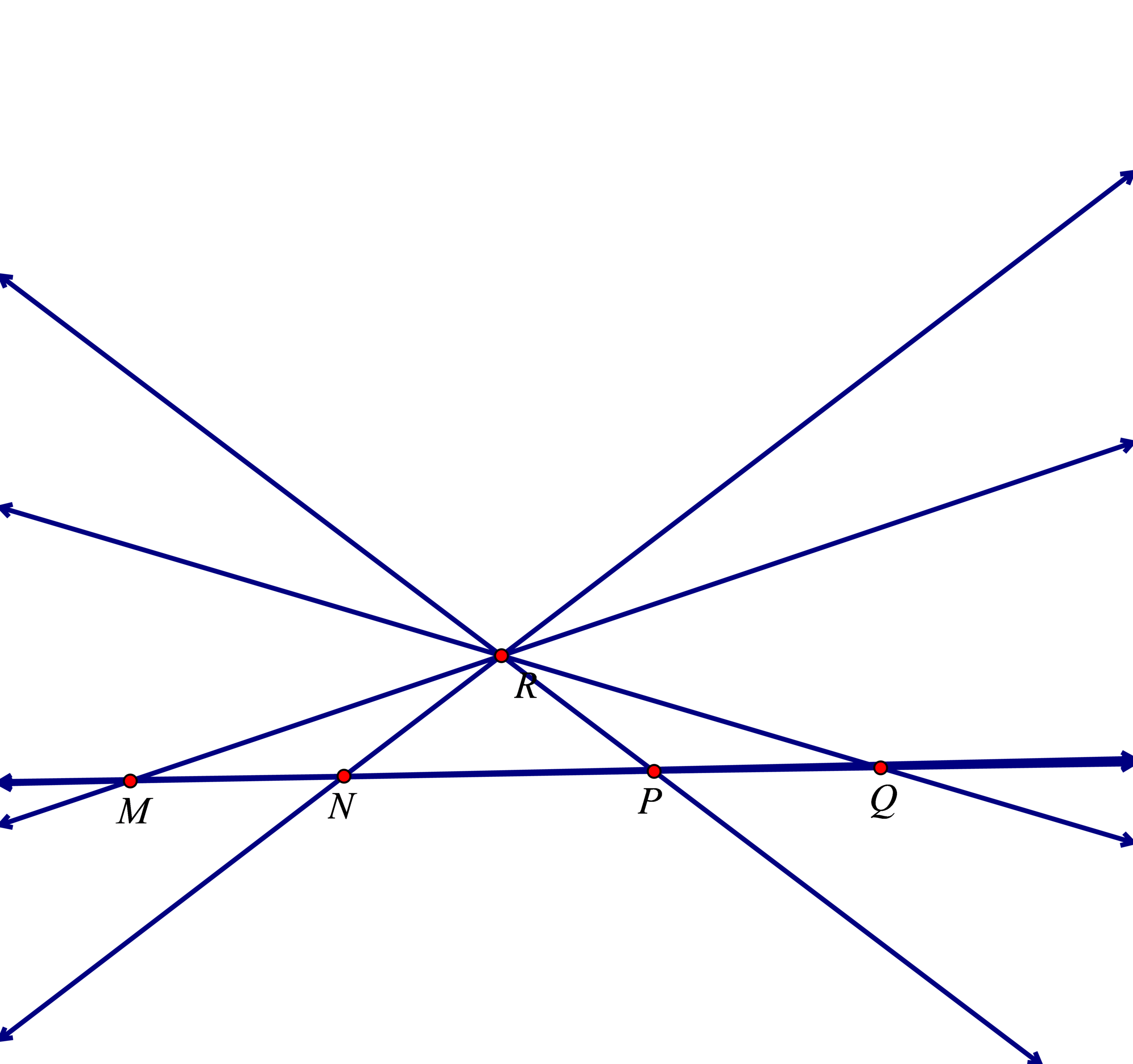
a) Có 5 đường thẳng, đó là đường thẳng MQ, RM, RN, RP, RQ.
b) Các tia gốc P là: PM, PN, PQ, PR. Hai tia PM, PN trùng nhau. Hai tia PM, PQ đối nhau.

6 tháng 7 2015
Cứ mỗi 1 cặp thì vẽ được 1 đường thẳng
=>9 điểm thì được 4 cặp và 1 điểm
vì đề bảo các cặp => 4x1=4(đường thẳng)
VH
25 tháng 11 2015
xét đề bài ta thấy: Có 2 trường hợp xảy ra:
1. Sẽ có 2 điểm thẳng hàng khác 5 điểm đã cho
Lúc có tất cả 23 đường thẳng
2.Tất cả điểm còn lại không thẳng hàng
Lúc đó sẽ có tất cả 27 đường thẳng

25 tháng 3 2023
Số đường thẳng vẽ được là:
1+3*17+\(C^3_{17}=732\left(đường\right)\)

a: TH1: Chọn 1 điểm trong 2 điểm M,N; 1 điểm trong 3 điểm P,Q,R
Số cách chọn 1 điểm trong 2 điểm M,N là 2 cách
Số cách chọn 1 điểm trong 3 điểm P,Q,R là 3 cách
=>Có 2*3=6(cách)
TH2: Vẽ đường thẳng PQR
=>Có 1 cách
TH3: Vẽ đường thẳng MN
=>Có 1 cách
Tổng số đường thẳng là:
6+1+1=8(đường)
b: TH1: Chọn 1 điểm trong 5 điểm thẳng hàng, chọn 1 điểm trong 4 điểm không thẳng hàng
Số cách chọn 1 điểm trong 5 điểm thẳng hàng là 5 cách
Số cách chọn 1 điểm trong 4 điểm không thẳng hàng là 4 cách
=>Có 5*4=20 đường thẳng
TH2: Vẽ 1 đường thẳng đi qua 5 điểm thẳng hàng
=>Có 1 đường thẳng
TH3: Chọn 2 điểm trong 4 điểm không thẳng hàng
=>Có \(C^2_4=6\left(đường\right)\)
Số đường thẳng tất cả là:
20+1+6=27(đường)