một công ty cần tuyển 2 nhân viên. Có 6 người nộp đơn trong đó có 4 nữ và 2 nam. Khả năng được tuyển của mỗi người như nhau. Giả sử Hoa là 1 trong 4 nữ. Tính xác suất để Hoa được tuyển biết rằng đã có nữ được tuyển
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
The đề bài ta có C n − 2 2 C n 4 = 2 C n − 2 4 C n 4 ⇔ n = 7 .

Đáp án A
Số cách lấy ra 4 ứng viên bất kỳ từ 16 ứng viên là ![]() cách.
cách.
- Gọi A là biến cố “4 ứng viên lấy được có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi”. Ta xét ba khả năng sau:
- Số cách lấy 1 10 tuổi, 3 11 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 2 11 tuổi, 1 12 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 1 11 tuổi, 2 12 tuổi là: ![]()
Xác suất của biến cố A là 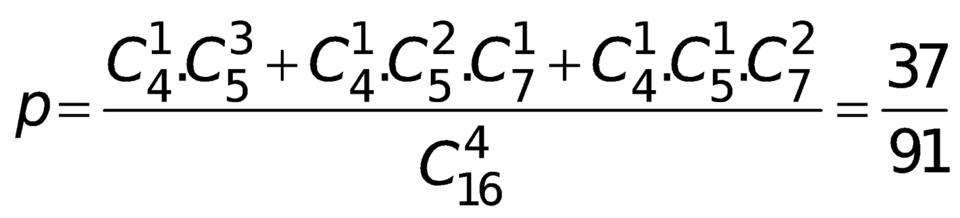 .
.

11111111111111111111111111111111111111111111111111111111119999999999999999999999999999999999999999999999999999+2222222222222222222222222222222222222222222222999999999999999999999999999999999=bao nhiêu giúp mình với

Không gian mẫu: \(12!\)
Xếp 8 nam: có \(8!\) cách
8 nam tạo thành 9 khe trống, xếp 4 nữ vào 9 khe trống này: \(A_9^4\) cách
\(\Rightarrow8!.A_9^4\) cách
Xác suất: \(P=\dfrac{8!.A_9^4}{12!}=\)
Câu này có thể coi như không giải theo cách gián tiếp được (thực ra là có giải được nhưng ko ai giải kiểu đó hết), nó bao gồm các trường hợp 4 nữ cạnh nhau, 3 nữ cạnh nhau, 2 nữ cạnh nhau, trong đó trường hợp trước còn bao hàm trường hợp sau cần loại trừ nữa

n(omega)=12!
A: "Xếp các học sinh thành 1 hàng ngang sao cho ko có 2 học sinh nữ nào đứng cạnh nhau"
=>\(n\left(A\right)=8!\cdot A^4_9\)
=>P=14/55
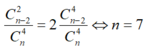

Đã có 1 nữ được tuyển nên số nữ còn lại là 4-1=3 và số người còn lại là 6-1=5(người)
Số cách chọn 1 người trong 5 người còn lại là: 5(cách)
=>Xác suất để Hoa trúng tuyển là \(P=\dfrac{1}{5}\)=20%