cho nửa đường tròn (0) đường kính AB, vẽ bán kình CO vuông góc với AB . M là 1 điểm bất kì trên cung AC .BM cắt AC tại H, gọi K là chân đường vuông góc kẻ từ H đến AB a) chứng minh tứ giác BCHK nội tiếp c) kẻ CP vuông góc với BM. trên đoạn BM lấy điểm E sao cho BE=AM chứng minh CM*MP= Pe

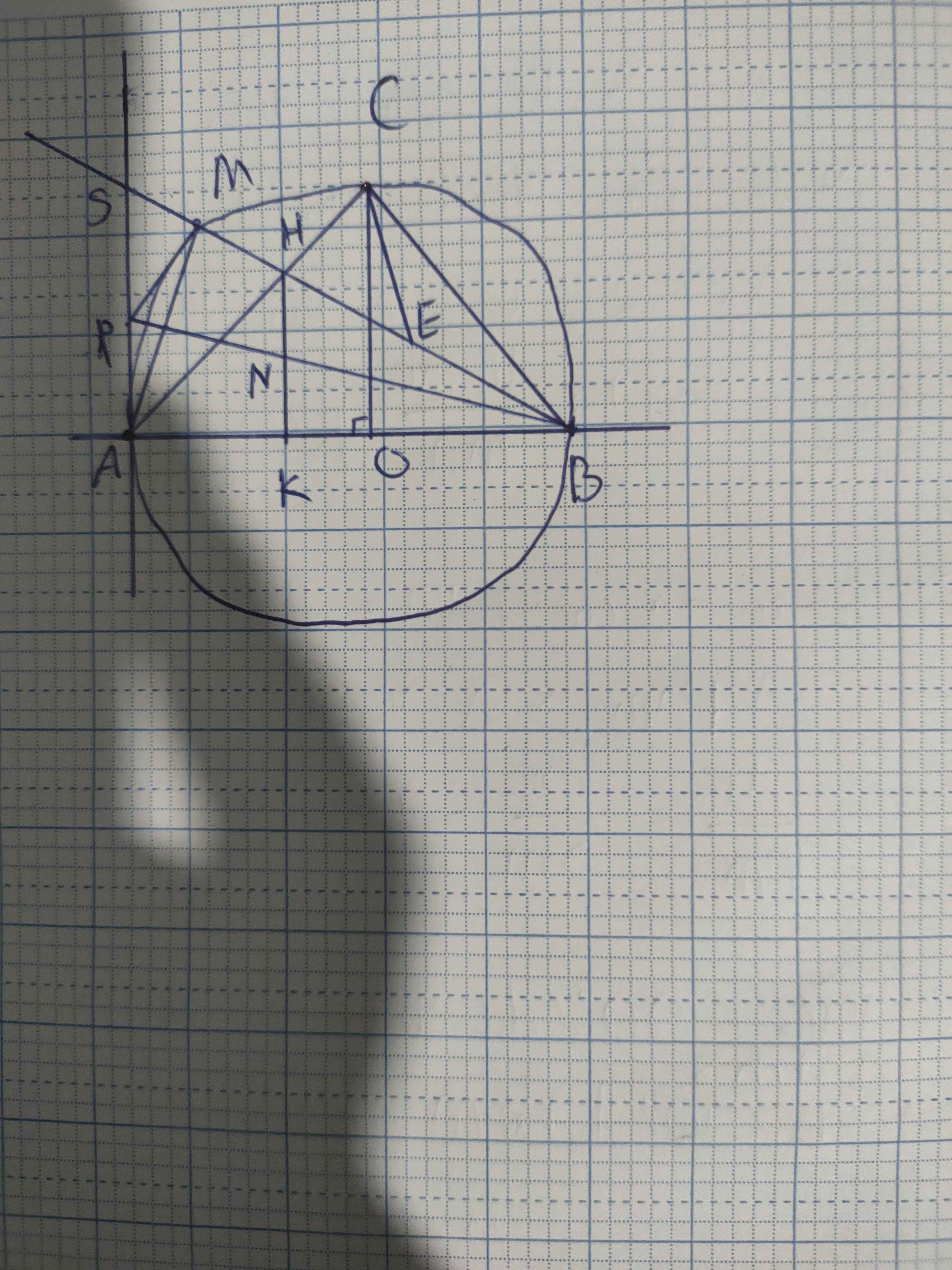


a) Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{HCB}=90^0\)
Xét tứ giác HKBC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: HKBC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)