(3a-1)(9a^2+3a+1)-(3a+1)(9a^2-3a+1)+2a+2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2b: \(=8\sqrt{2}-3\sqrt{2}-3\sqrt{2}-10\sqrt{2}=-8\sqrt{2}\)
3:
a: \(=\left(\sqrt{6a}+\dfrac{\sqrt{6a}}{3}+\sqrt{6a}\right):\sqrt{6a}\)
=1+1/3+1
=7/3
b: \(=\dfrac{2}{3a-1}\cdot\sqrt{3}\cdot a\cdot\left|3a-1\right|\)
\(=\dfrac{2\sqrt{3}\cdot a\left(1-3a\right)}{3a-1}=-2a\sqrt{3}\)

= \(\left(3a-1\right)^2\) + \(2\left(3a-1\right)\left(3a+1\right)\) + \(\left(3a-1\right)^2\)
= \(\left(3a-1+3a+1\right)^2\)
= \(\left(6a\right)^2\)
= \(36a^2\)
\(\left(3a-1\right)^2+2\left(9a^2-1\right)+\left(3a+1\right)^2\)
\(=\left(3a-1+3a+1\right)^2\)
\(=36a^2\)

a: Sửa đề: \(A=\left(3a-1\right)\left(9a^2+3a+1\right)-\left(3a+1\right)\left(9a^2-3a+1\right)+2a+2\)
\(=27a^3-1-27a^3-1+2a+2=2a=2\cdot5=10\)
b: \(=4x^2+2x+1-20x^3+10x^2+4x\)
\(=-20x^3+14x^2+6x+1\)
c: \(=5x^2-20xy-4y^2+20xy=5x^2-4y^2\)
\(=5\cdot\dfrac{1}{25}-4\cdot\dfrac{1}{4}=\dfrac{1}{5}-1=-\dfrac{4}{5}\)


Mình đã làm bài này bằng cách tìm a rồi thế vào M, mong bạn nào có cách giải hay hơn, gọn hơn xin giúp mình. Cảm ơn các bạn!!!

\(a;b>0\Rightarrow3a+2b+1>1\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\) đồng biến
Mà \(9a^2+b^2\ge2\sqrt{9a^2b^2}=6ab\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge2\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}log_{6ab+1}\left(3a+2b+1\right)=1\\3a=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6ab+1=3a+2b+1\\b=3a\end{matrix}\right.\)
\(\Rightarrow18a^2+1=3a+6a+1\)
\(\Leftrightarrow18a^2-9a=0\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)

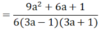
\(\left(3a-1\right)\left(9a^2+3a+1\right)-\left(3a+1\right)\left(9a^2-3a+1\right)+2a+2\)
\(=27a^3-1-\left(27a^3+1\right)+2a+2=27a^3-1-27a^3-1+2a+2\)
\(=-2+2a+2=2a\)