Cho phương trình x2 - mx - m - 1 = 0 ( m là tham số). Tìm các giá trị của m để phương trình 2x1 - 5x2 = -2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m-1)^2+2m+1=m^2+2\geq 0$
$\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=2(m-1)$
$x_1x_2=-2m-1$
Khi đó:
$2x_1+3x_2+3x_1x_2=-11$
$\Leftrightarrow 2(x_1+x_2)+3x_1x_2+x_2=-11$
$\Leftrightarrow 4(m-1)+3(-2m-1)+x_2=-11$
$\Leftrightarrow x_2=2m-4$
$x_1=2(m-1)-x_2=2m-2-(2m-4)=2$
$-2m-1=x_1x_2=2(2m-4)$
$\Leftrightarrow -2m-1=4m-8$
$\Leftrightarrow 7=6m$
$\Leftrightarrow m=\frac{7}{6}$

Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m-1)^2+2m+1=m^2+2\geq 0$
$\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=2(m-1)$
$x_1x_2=-2m-1$
Khi đó:
$2x_1+3x_2+3x_1x_2=-11$
$\Leftrightarrow 2(x_1+x_2)+3x_1x_2+x_2=-11$
$\Leftrightarrow 4(m-1)+3(-2m-1)+x_2=-11$
$\Leftrightarrow x_2=2m-4$
$x_1=2(m-1)-x_2=2m-2-(2m-4)=2$
$-2m-1=x_1x_2=2(2m-4)$
$\Leftrightarrow -2m-1=4m-8$
$\Leftrightarrow 7=6m$
$\Leftrightarrow m=\frac{7}{6}$

Lời giải:
Để pt có 2 nghiệm thì:
$\Delta'=(m-1)^2+2m-5\geq 0$
$\Leftrightarrow m^2-4\geq 0$
$\Leftrightarrow m\geq 2$ hoặc $m\leq -2$
Áp dụng định lý Viet: \(\left\{\begin{matrix}
x_1+x_2=2(1-m)\\
x_1x_2=-2m+5\end{matrix}\right.\)
\(2x_1+3x_2=-5\)
\(\Leftrightarrow 2(x_1+x_2)+x_2=-5\Leftrightarrow 4(1-m)+x_2=-5\)
\(\Leftrightarrow x_2=4m-9\)
\(x_1=2(1-m)-x_2=11-6m\)
$x_1x_2=-2m+5$
$\Leftrightarrow (4m-9)(11-6m)=-2m+5$
Giải pt này suy ra $m=2$ hoặc $m=\frac{13}{6}$ (đều thỏa mãn)

a) Với m= 2, ta có phương trình: x 2 + 2 x − 3 = 0
Ta có: a + b + c = 1 + 2 − 3 = 0
Theo định lý Viet, phương trình có 2 nghiệm:
x 1 = 1 ; x 2 = − 3 ⇒ S = 1 ; − 3 .
b) Chứng minh rằng phương trình luôn có nghiệm ∀ m .
Ta có: Δ ' = m − 1 2 − 1 + 2 m = m 2 ≥ 0 ; ∀ m
Vậy phương trình luôn có nghiệm ∀ m .
c) Theo định lý Viet, ta có: x 1 + x 2 = − 2 m + 2 x 1 . x 2 = 1 − 2 m
Ta có:
x 1 2 . x 2 + x 1 . x 2 2 = 2 x 1 . x 2 + 3 ⇔ x 1 . x 2 x 1 + x 2 − 2 = 6 ⇒ 1 − 2 m − 2 m + 2 − 2 = 6 ⇔ 2 m 2 − m − 3 = 0
Ta có: a − b + c = 2 + 1 − 3 = 0 ⇒ m 1 = − 1 ; m 2 = 3 2
Vậy m= -1 hoặc m= 3/2

b: \(\text{Δ}=\left(2m+3\right)^2-4\left(4m+2\right)\)
\(=4m^2+12m+9-16m-8\)
\(=4m^2-4m+1=\left(2m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm
Theo đề, ta có:
\(\left\{{}\begin{matrix}2x_1-5x_2=6\\x_1+x_2=2m+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1-5x_2=6\\2x_1+2x_2=4m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7x_2=-4m\\2x_1=5x_2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\2x_1=\dfrac{20}{7}m+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4}{7}m\\x_1=\dfrac{10}{7}m+3\end{matrix}\right.\)
Theo đề, ta có: \(x_1x_2=4m+2\)
\(\Rightarrow4m+2=\dfrac{40}{49}m^2+\dfrac{12}{7}m\)
\(\Leftrightarrow m^2\cdot\dfrac{40}{49}-\dfrac{16}{7}m-2=0\)
\(\Leftrightarrow40m^2-112m-98=0\)
\(\Leftrightarrow40m^2-140m+28m-98=0\)
=>\(20m\left(2m-7\right)+14\left(2m-7\right)=0\)
=>(2m-7)(20m+14)=0
=>m=7/2 hoặc m=-7/10

\(\Delta=m^2-4\left(m-4\right)=\left(m^2-4m+4\right)+12=\left(m-2\right)^2+12>0;\forall m\)
Suy ra pt luôn có hai nghiệm pb với mọi m
Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-4\end{matrix}\right.\)
\(\left(5x_1-1\right)\left(5x_2-1\right)< 0\)
\(\Leftrightarrow25x_1x_2-5\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow25\left(m-4\right)-5m+1< 0\)
\(\Leftrightarrow m< \dfrac{99}{20}\)
Vậy...
\(\Delta=m^2-4m+16=\left(m-2\right)^2+12>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-4\end{matrix}\right.\)
Ta có: \(\left(5x_1-1\right)\left(5x_2-1\right)=25x_1x_2-5\left(x_1+x_2\right)+1\)
\(=25\left(m-4\right)-5m+1=20m-99\)
\(\Rightarrow20m-99< 0\Rightarrow m< \dfrac{99}{20}\)

\(\Delta=\left(2m+4\right)^2-4\left(3m+2\right)\)
\(=4m^2+16m+16-12m-8\)
\(=4m^2+4m+8\)
\(=\left(2m+1\right)^2+7>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\x_1x_2=3m+2\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=2m+4\\-2x_1+x_2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2m+1\\x_1+x_2=2m+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2}{3}m+\dfrac{1}{3}\\x_2=2m+4-\dfrac{2}{3}m-\dfrac{1}{3}=\dfrac{4}{3}m+\dfrac{11}{3}\end{matrix}\right.\)
Ta có: \(x_1x_2=3m+2\)
nên \(\left(\dfrac{2}{3}m+\dfrac{1}{3}\right)\left(\dfrac{4}{3}m+\dfrac{11}{3}\right)=3m+2\)
\(\Leftrightarrow m^2\cdot\dfrac{8}{9}+\dfrac{22}{9}m+\dfrac{4}{9}m+\dfrac{11}{9}=3m+2\)
\(\Leftrightarrow m^2\cdot\dfrac{8}{9}-\dfrac{1}{9}m-\dfrac{7}{9}=0\)
\(\Leftrightarrow8m^2-m-7=0\)
\(\Leftrightarrow\left(m-1\right)\left(8m+7\right)=0\)
=>m=1 hoặc m=-7/8

\(\Delta=\left(-m\right)^2-2.1.\left(m-1\right)\\ =m^2-2m+1\\ =\left(m-1\right)^2\)
Phương trình có hai nghiệm phân biệt :
\(\Leftrightarrow\Delta>0\\ \Rightarrow\left(m-1\right)^2>0\\ \Rightarrow m\ne1\)
Theo vi ét :
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x^2_1+x^2_2=x_1+x_2\\ \Leftrightarrow x^2_1+x^2_2=m\\ \Leftrightarrow\left(x^2_1+2x_1x_2+x_2^2\right)-2x_1x_2=m\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-m=0\\ \Leftrightarrow m^2-2\left(m-1\right)-m=0\\ \Leftrightarrow m^2-2m+2-m=0\\ \Leftrightarrow m^2-3m+2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=2\left(t/m\right)\end{matrix}\right.\)
Vậy \(m=2\)
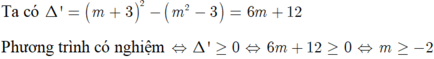
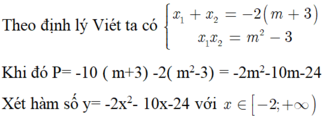
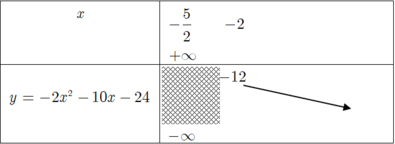

\(\Delta=m^2-4\left(-m-1\right)=m^2+4m+4=\left(m+2\right)^2\ge0\)
Để pt có 2 nghiệm pb khi m khác -2
Theo Vi et \(\hept{\begin{cases}x_1+x_2=m\left(1\right)\\x_1x_2=-m-1\left(2\right)\end{cases}}\)
Ta có \(2x_1-5x_2=-2\left(3\right)\)
Từ (1) ; (3) ta có \(\hept{\begin{cases}2x_1+2x_2=2m\\2x_1-5x_2=-2\end{cases}}\Leftrightarrow\hept{\begin{cases}7x_2=2m+2\\x_1=m-x_2\end{cases}}\Leftrightarrow\hept{\begin{cases}x_2=\frac{2m+2}{7}\\x_1=\frac{5m-2}{7}\end{cases}}\)
Thay vào (2) ta được \(\frac{\left(2m+2\right)\left(5m-2\right)}{49}=-m-1\)
\(\Leftrightarrow10m^2+6m-4=-49m-49\)
\(\Leftrightarrow10m^2+55m+45=0\Leftrightarrow m=-1;m=-\frac{9}{2}\)(tm)