Giúp e giải chỉ tiết đi mn ơi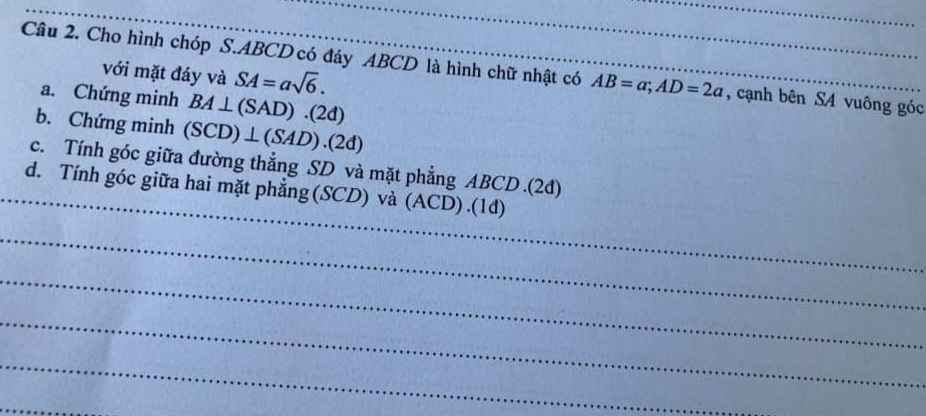
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\left(x^7+x\right)^3\)
\(y'=3\left(x^7+x\right)^2.\left(x^7+x\right)'=3\left(x^7+x\right)^2\left(7x^6+1\right)\)

7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)

ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}

7.
\(y'=\left(-x^3\right)'-\left(5x\right)'+\left(2\right)'=-3x^2-5\)
\(y''=\left(-3x^2\right)'-\left(5\right)'=-6x\)
8.
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+3x-2\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)\)
Do: \(\lim\limits_{x\rightarrow+\infty}x^3=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=1>0\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x^2}-\dfrac{2}{x^3}\right)=+\infty\)

Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....

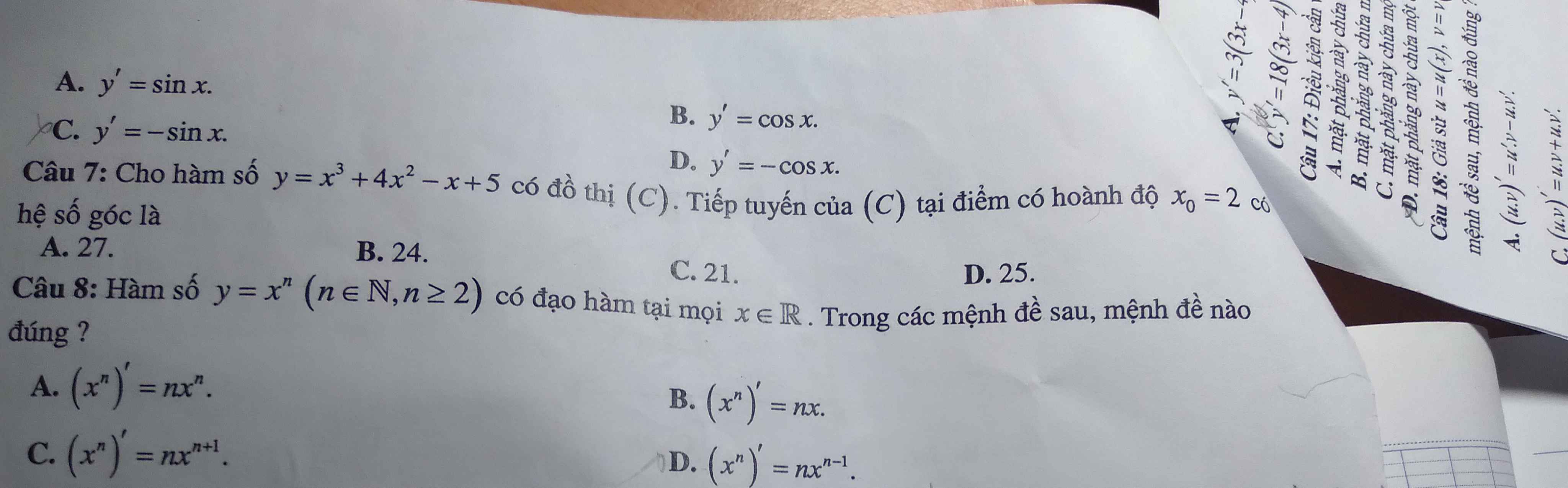
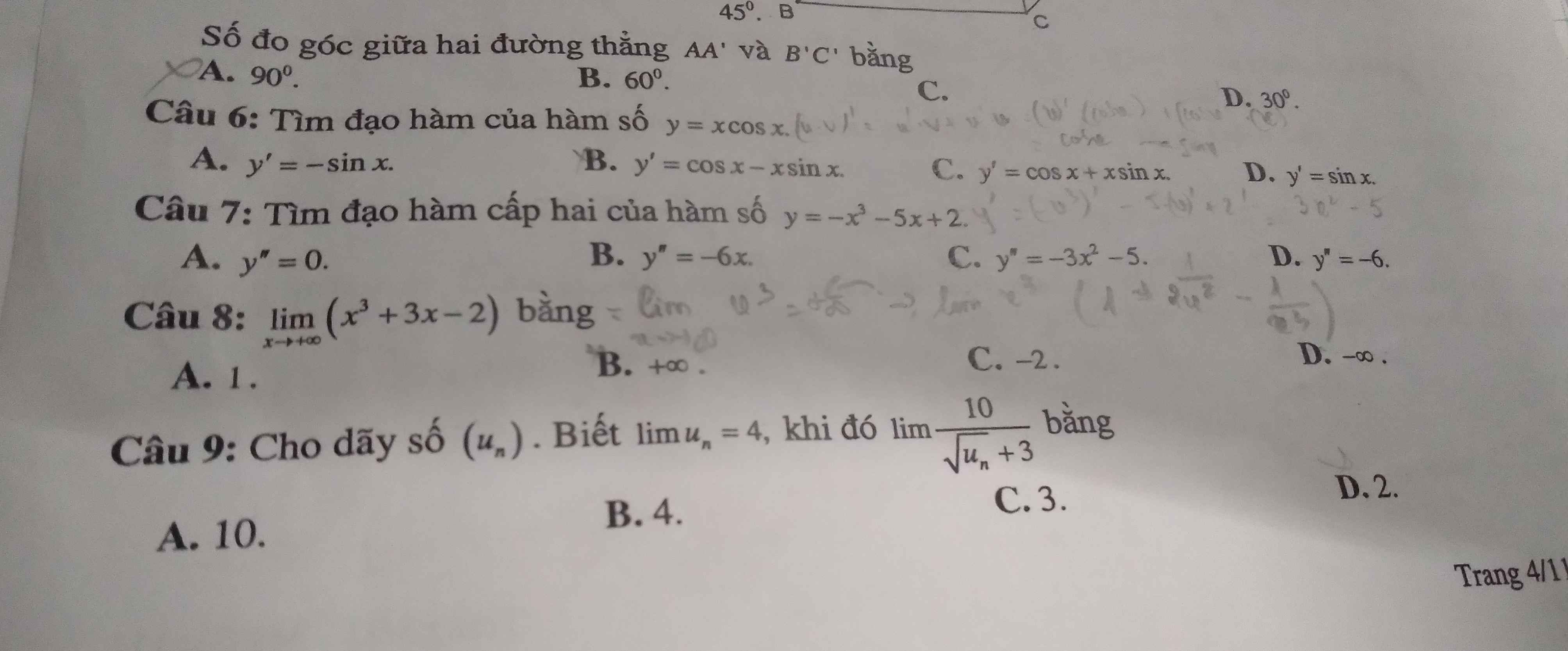



a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
b.
Ta có \(CD||AB\) (do ABCD là hcn)
Mà \(AB\perp\left(SAD\right)\Rightarrow CD\perp\left(SAD\right)\)
Lại có \(CD\in\left(SCD\right)\)
\(\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SDA}\approx50^046'\)
d.
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp\left(ACD\right)\)
Mà \(SA\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(ACD\right)\) (1)
Theo câu b ta có: \(\left(SAD\right)\perp\left(SCD\right)\) (2)
(1);(2) \(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ACD)
Theo câu c ta có: \(\widehat{SDA}=50^046'\)