Từ một điểm A nằm ngoài đường tròn (O), kẻ 2 tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên tia đối của tia BC lấy điểm D. Gọi E là giao điểm của DO với AC. Qua E kẻ tiếp tuyến thứ hai với đường tròn, tiếp tuyến này cắt đường thẳng AB tại K. Chứng minh rằng 4 điểm D, B, O, K cùng thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét (O):
D đối xứng với B qua O (gt).
\(\Rightarrow\) O là trung điểm của BD.
\(\Rightarrow\) BD là đường kính của (O).
Xét (O):
BD là đường kính của (O) (cmt).
\(E\in\left(O\right)\left(gt\right).\)
\(\Rightarrow\widehat{BED}=90^o.\)
Xét (O):
AB là tiếp tuyến (gt).
\(\Rightarrow BD\perp AB\) (Tính chất tiếp tuyến).
\(\Rightarrow\widehat{ABD}=90^o.\)
Xét \(\Delta ADB\) và \(\Delta BDE:\)
\(\widehat{ABD}=\widehat{BED}\left(=90^o\right).\\ \widehat{ADB}chung.\)
\(\Rightarrow\dfrac{BD}{DE}=\dfrac{AB}{BE}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow BD.BE=BA.DE.\)


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

\(a,\) Ta có \(OB=OC=R;AB=AC\Rightarrow OA\) là trung trực BC
Do đó \(OA\bot BC=\left\{H\right\}\)
Áp dụng HTL: \(OB^2=OH\cdot OA\Rightarrow OD^2=OH\cdot OA\Rightarrow\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\Rightarrow\Delta OHD\sim\Delta ODA\left(c.g.c\right)\)
\(b,\) Gọi \(\left\{I\right\}=BC\cap AE\)
\(\widehat{OHD}=\widehat{ODA}\Rightarrow\widehat{DHA}=\widehat{ODE}=\widehat{OED}\) (cùng bù với 2 góc bằng nhau, \(\Delta ODE\) cân tại O)
\(\Rightarrow\Delta AEO\sim\Delta AHD\left(g.g\right)\\ \Rightarrow\widehat{AOE}=\widehat{ADH}\)
Mà \(\dfrac{OH}{DH}=\dfrac{OD}{AD}\left(\Delta OHD\sim\Delta ODA\right)\Rightarrow\dfrac{OH}{DH}=\dfrac{OE}{AD}\)
\(\Rightarrow\Delta HEO\sim\Delta HDA\left(g.g\right)\\ \Rightarrow\widehat{OHE}=\widehat{DHA}\)
Mà \(OA\bot BC\Rightarrow\widehat{IHE}=\widehat{IHD}\)
Vậy BC trùng với p/g \(\widehat{DHE}\)
\(c,\) Vì HI là p/g trong của \(\Delta DHE\) và \(HA\bot HI\)
\(\Rightarrow HA\) là p/g ngoài
\(\Rightarrow\dfrac{IE}{ID}=\dfrac{AE}{AD}=\dfrac{HE}{HD}\left(1\right)\)
Mà \(MN\text{//}BE\Rightarrow\dfrac{MD}{BE}=\dfrac{AD}{AE};\dfrac{ND}{BE}=\dfrac{ID}{IE}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow MD=MN\RightarrowĐpcm\)

1) Hình vẽ câu 1) đúng
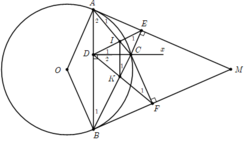
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

Đáp án B
* Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB = AC; DB = DM; EM = EC
suy ra: DE = DM + ME = DB + EC.
* Chu vi tam giác ADE là:
AD + AE + DE = AD + AE + DB + EC
= (AD + DB ) + ( AE + EC ) = AB + AC = 2AB ( vì AB = AC )
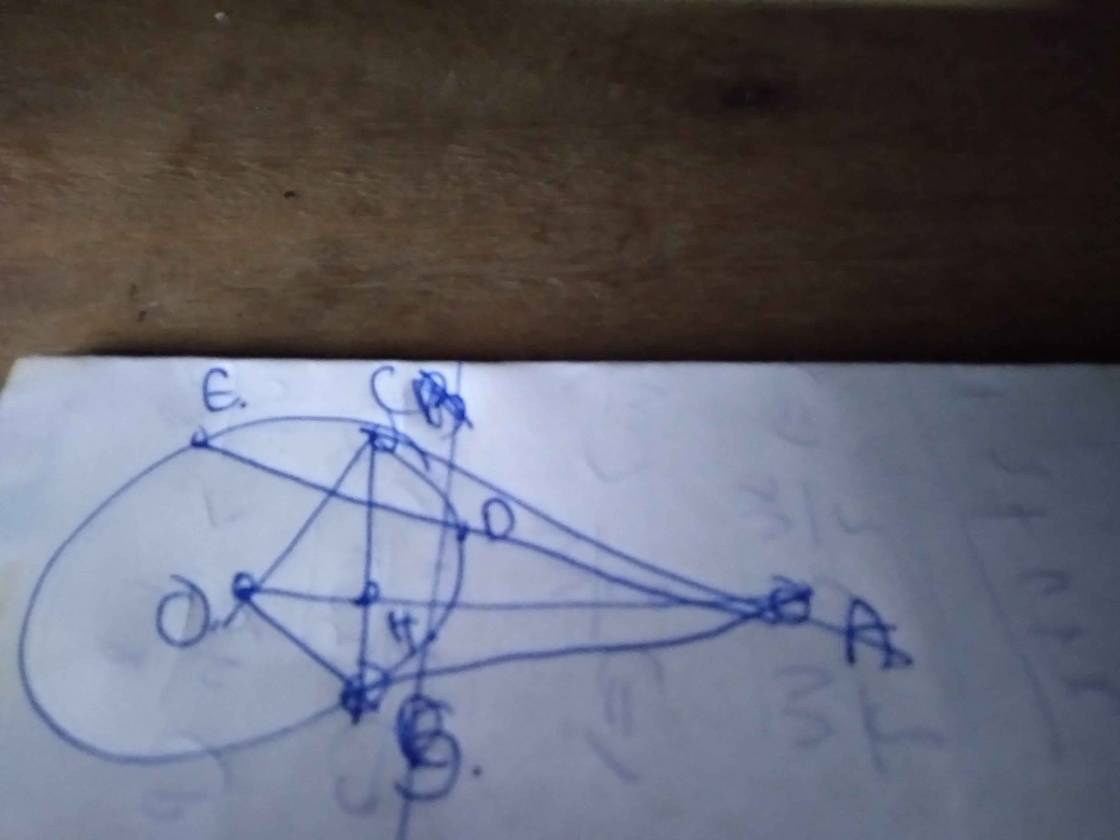
Mình đang thắc mắc chỗ chứng minh \(\widehat{EOC}=\widehat{ECD}\), còn mấy chỗ còn lại mình làm được rồi.