MÌNH SẮP NỘP BÀI RỒI Ạ!!!
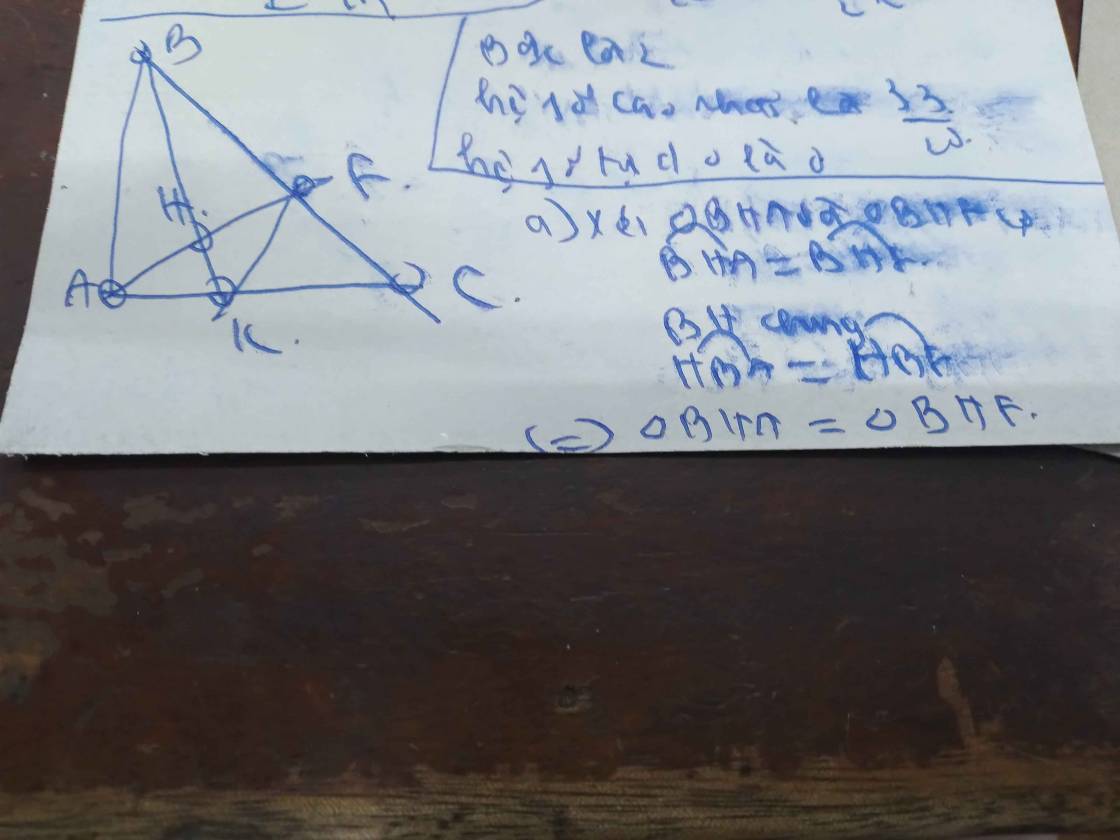
Cho tam giác ABC vuông tại A, kẻ phân giác BK của góc B (K thuộc AC ), kẻ AE vuông góc với BK tại H và E thuộc BC
a.chứng minh : tam giác BHA = tam giác BHE
b. chứng minh : EK vuông góc BC
c. chứng minh : AK<KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc ABH=góc EBH
=>ΔBHA=ΔBHE
c: ΔBHA=ΔBHE
=>BA=BE
Xét ΔBAK và ΔBEK có
BA=BK
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=góc BAK=90 độ
=>EK vuông góc bC
d: AK=KE
KE<KC
=>AK<KC

a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc HBA=góc HBE
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>KE vuông góc BC

a/
Xét tg BAE và tg BKE có
BE chung; BA=BK (gt)
\(\widehat{ABE}=\widehat{KBE}\left(gt\right)\)
=> tg BAE = tg BKE (c.g.c)
b/
Ta có tg BAE = tg BKE (cmt) => AE=KE và \(\widehat{BAE}=\widehat{BKE}=90^o\)
\(\Rightarrow EK\perp BC\)
c/
Xét tg vuông CKE có EC là cạnh huyền => KE<EC (trong tg vuông cạnh huyền là cạnh có độ dài lớn nhất)
Mà AE=KE (cmt)
=> AE<EC
d/ Gọi D là giao của BE với AK
Xét tg ABK có
BA=BK => tg ABK cân tại B
BD là phân giác \(\widehat{ABK}\)
=> BD là trung tuyến của tg ABK (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường trung tuyến)
Có AI là trung tuyến của tg ABK
=> G là trong tâm của tg ABK => BG=2.DG
Xét tg DKG có
\(DK=DA=\dfrac{AK}{2}\) (BD là trung tuyến)
Ta có
\(DG+DK>KG\) (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
\(\Rightarrow DG+\dfrac{AK}{2}>KG\) Mà \(BG=2.DG\Rightarrow BG>DG\Rightarrow BG+\dfrac{AK}{2}>KG\)

aXét 2 tam giác BHA và tam giác BHE có:
H1=H2=90
B1=B2(phân giác góc B)
BH chung
=> tam giác BHA = tam giác BHE(g.c.g)
b Chứng minh AK // DE mà
MÀ AK vuông góc vs BC
=> ED vuông góc vs BC

a, Xét △BHA vuông tại H và △BHE vuông tại H
Có: BH là cạnh chung
ABH = EBH (gt)
=> △BHA = △BHE (cgv-gn)
b, Vì △BHA = △BHE (cmt) => BA = BE (2 cạnh tương ứng)
Xét △BAD và △BED
Có: AB = BE (cmt)
ABD = EBD (gt)
BD là cạnh chung
=> △BAD = △BED (c.g.c)
=> BAD = BED (2 góc tương ứng)
Mà BAD = 90o
=> BED = 90o
=> DE ⊥ BE
=> DE ⊥ BC
c, Vì △BAD = △BED (cmt) => AD = ED (2 cạnh tương ứng)
Xét △EDC vuông tại E có: DE < DC (cạnh góc vuông nhỏ hơn cạnh huyền)
=> AD < DC
d, Ta có: AD = ED (cmt) => △ADE vuông tại D => DAE = DEA
Vì AK ⊥ BC (gt) và DE ⊥ BC (cmt)
=> AK // DE (từ vuông góc đến song song)
=> KAE = AED (2 góc so le trong)
mà DAE = DEA (cmt)
=> KAE = DAE => KAE = CAE
Mà AE nằm giữa AK, AC
=> AE là phân giác CAK

Xin chào bạn. Tôi là Maria. Tôi đã chết trong một vụ tai nạn năm tôi 8 tuổi. Bạn phải đọc hết tin nhắn này nếu không bạn sẽ gặp xui xẻo cả đời. Hiện tại thì tôi có thể đang ở rất gần bạn và tôi yêu cầu bạn phải chia sẻ tin nhắn này cho 20 người nữa. Nếu không làm được, bạn sẽ chết. Ví dụ 1: Có một chàng trai tên là Jake, anh ấy đọc được tin nhắn này. Nhưng anh đã cười nhạo và không chia sẻ cho 20 người nên vào 2 giờ sáng, anh ấy đã chết do một vụ tai nạn. Một cái chết giống y hệt của tôi. Là tôi làm đấy! Ví dụ 2: Một có gái trẻ tên là Sabrina. Cô cũng nhận được dòng tin nhắn này nhưng cô chỉ chia sẻ cho 10 người và cô đã gặp ác mộng suốt phần đời còn lại. Thêm một ví dụ nữa: Có ba người bạn thân và họ tên là Tina Mersa, Sarah Ri và Chris Na. Họ đang chơi đùa vui vẻ thì nhận được những dòng tin nhắn này và họ đã gửi ngay cho 20 người. Vậy là họ trở thành những con người may mắn. Họ được mọi người yêu quý, điểm số của họ cũng rất cao. Vậy bạn muốn giống ai? Hãy gửi tiếp cho 20 người để được may mắn hoặc không thì bạn sẽ xui xẻo hoặc chết. Trò chơi sẽ bắt đầu từ lúc bạn đọc những dòng tin nhắn này. CHÚC BẠN MAY MẮN!