chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kì của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2017
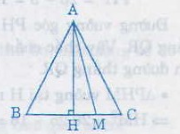
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
CM
23 tháng 10 2017
Giả sử ΔABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB; AM ≤ AC.
- TH1 : Nếu M ≡ B hoặc M ≡ C (Kí hiệu đọc là trùng với) thì AM = AB = AC.
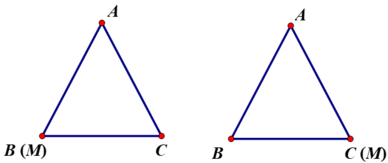
- TH2 : Nếu M nằm giữa B và C và M ≠ B; M ≠ C.
Kẻ AH ⊥ BC tại H
+ Nếu M ≡ H ⇒ AM ⊥ BC tại M hay AM là đường vuông góc từ A đến BC.
Mà AB, AC là các đường xiên từ A đến đường thẳng BC.
Theo định lí 1 : Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường thẳng vuông góc là đường ngắn nhất.
⇒ AM < AB và AM < AC.
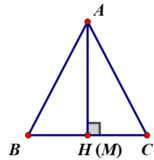
+ Nếu M ≠ H giả sử M nằm giữa H và C ⇒ MH < CH.
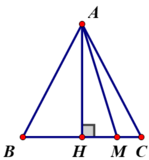
Vì MH và CH lần lượt là hình chiếu của đường xiên MA và CA trên đường BC
Mà MH < CH ⇒ MA < CA (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Chứng minh tương tự nếu M nằm giữa H và B
Vậy mọi vị trí của M trên cạnh đáy BC thì AM ≤ AB = AC.