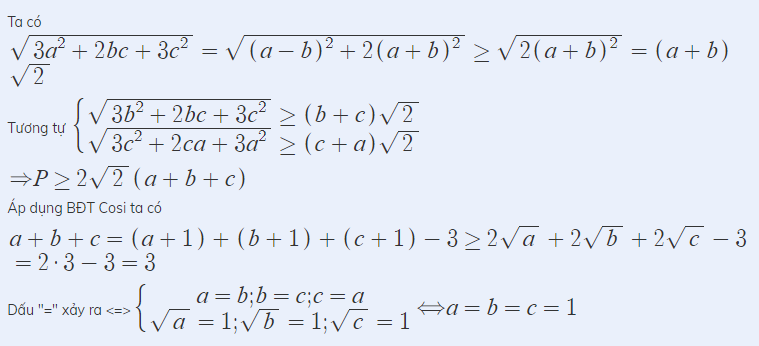Câu hỏi của Doãn Thị Thu Trang - Toán lớp 7 - Học toán với OnlineMath

xin lỗi nha MÌNH sai đề ở chổ \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)

\(3x^2+2xy+3y^2=\left(x+y\right)^2+2\left(x^2+y^2\right)\ge\left(x+y\right)^2+\left(x+y\right)^2=2\left(x+y\right)^2\)

\(\Rightarrow A\ge\sqrt{2}\left(a+b\right)+\sqrt{2}\left(b+c\right)+\sqrt{2}\left(c+a\right)\)

\(A\ge2\sqrt{2}\left(a+b+c\right)\ge\frac{2\sqrt{2}}{3}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=6\sqrt{2}\)

\(A_{min}=6\sqrt{2}\) khi \(a=b=c=1\)

Đặt a/b=c/d=k

=>a=bk; c=dk

\(\dfrac{a^2}{b^2}=\dfrac{b^2k^2}{b^2}=k^2\)

\(\dfrac{3a^2-2ac}{3b^2-2bd}=\dfrac{3\cdot b^2k^2-2\cdot bk\cdot dk}{3b^2-2bk}=k^2\)

Do đó: \(\dfrac{a^2}{b^2}=\dfrac{3a^2-2ac}{3b^2-2bd}\)

Mk nghĩ đề sai nhé

Lời giải

Vì \(a;b;c\) là các cạnh của tam giác nên \(a;b;c>0\)

Ta luôn có: \(\left\{{}\begin{matrix}a^2+b^2\ge2ab\\b^2+c^2\ge2bc\\c^2+a^2\ge2ac\end{matrix}\right.\)

Cộng theo 3 vế ta có: \(a^2+b^2+b^2+c^2+c^2+a^2\ge2ab+2bc+2ac\)

\(\Rightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ac\right)\)

\(\Rightarrow a^2+b^2+c^2\ge ab+bc+ac\)

Dấu "=" xảy ra khi: \(a=b=c\Leftrightarrow\Delta ABC\) đều

cái này thì mk làm đc rồi mk cũng nghĩ giống bạn đề sai

Bài 1:

Giải:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{a}{b}=\frac{c}{d}=\frac{3a}{3b}=\frac{2c}{2d}=\frac{3a+2c}{3b+2d}\)

\(\Rightarrow\frac{a}{b}=\frac{c}{d}=\frac{3a+2c}{3b+2d}\)

Vậy \(\frac{a}{b}=\frac{c}{d}=\frac{3a+2c}{3b+2d}\)

Bài 2:

Giải:

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)

\(\Rightarrow a=bk,c=dk\)

Ta có: \(\frac{ac}{bd}=\frac{bkdk}{bd}=k^2\) (1)

\(\frac{a^2-c^2}{b^2-d^2}=\frac{\left(bk\right)^2-\left(dk\right)^2}{b^2-d^2}=\frac{b^2.k^2-d^2.k^2}{b^2-d^2}=\frac{k^2.\left(b^2-d^2\right)}{b^2-d^2}=k^2\) (2)

Từ (1) và (2) suy ra \(\frac{ac}{bd}=\frac{a^2-c^2}{b^2-d^2}\)

Bài 3: Tương tự nhé bạn chỉ cần thay a = bk, c = dk vào thôi