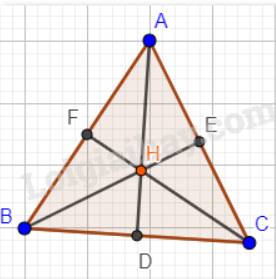
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.

Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.

Suy ra: AF = BF = AE = CE = BD = CD;

\(AD \bot BC; BE \bot AC; CF \bot AB\)

Xét tam giác ADB và tam giác ADC có:

     AD chung

    \(\widehat{ADB}=\widehat{ADC} (=90^0)\)

     BD = CD (D là trung điểm của đoạn thẳng BC).

Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).

Tương tự, ta cũng được, AC = BC

Xét tam giác ABC có AB = AC = BC nên là tam giác đều.

Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC, BH ⊥ AC, CH ⊥ AB

Trong ΔAHB, ta có:

       AC ⊥ BH

       BC ⊥ AH

Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

       AB ⊥ CH

       CB ⊥ AH

Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

       BA ⊥ HC

       CA ⊥ BH

Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

Giải

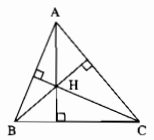
Trong ∆ABC ta có H là trực tâm nên

\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)

Trong ∆AHB ta có:

Hai đường cao kẻ từ A và B cắt nhau tại C.

Vậy C là trực tâm của ∆AHB.

Trong ∆HAC ta có:

Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.

Trong ∆HBC ta có:

Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.

Tham khảo:

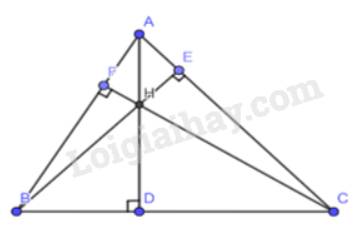
+) Xét tam giác HBC ta có :

HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC

BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC

CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC

Ta kéo dài HD, BF, CE sẽ cắt nhau tại A

\( \Rightarrow \) A là trực tâm tam giác HBC

+) Xét tam giác HAB ta có :

HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB

BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB

BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB

Ta kéo dài HF, BD, AE sẽ cắt nhau tại C

\( \Rightarrow \) C là trực tâm tam giác HAB

+) Xét tam giác HAC ta có :

HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC

AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC

CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC

Ta kéo dài CD, HE, AF sẽ cắt nhau tại B

\( \Rightarrow \) B là trực tâm tam giác HAC.

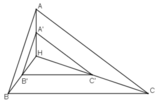
+ ΔABC nhọn ⇒ trực tâm H nằm trong ΔABC.

+ Gọi A’ = V(H; ½) (A)

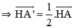
⇒ A’ là trung điểm AH.

+ Tương tự :

B’ = V(H; ½) (B) là trung điểm BH.

C’ = V(H; ½) (C) là trung điểm CH.

⇒ V(H; ½)(ΔABC) = ΔA’B’C’ với A’; B’; C’ là trung điểm AH; BH; CH.

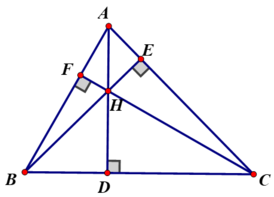
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.

⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.

 ΔHBC có :

AD ⊥ BC nên AD là đường cao từ H đến BC.

BA ⊥ HC tại F nên BA là đường cao từ B đến HC

CA ⊥ BH tại E nên CA là đường cao từ C đến HB.

AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.