Cho hai đoạn thẳng AB,CD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn.
a)Chứng minh rằng các đoạn thẳng AC,CB,BD,DA bằng nhau.
b)Tìm tia phân giác của các góc (khác góc bẹt) trong hình vẽ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 4 2019
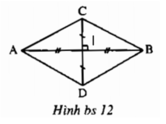
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB.
+) Xét tam giác ACI và tam giác ADI có:
AI chung
CI = DI (vì I là trung điểm của CD).
∠AIC = ∠ DIA = 90º ( vì AB vuông góc với CD tại I).
Suy ra: ∆ ACI = ∆ ADI (c.g.c)
Suy ra: ∠CAI = ∠ ADI ( hai góc tương ứng).
Do đó, AB là tia phân giác của góc ∠CAD .
+) Chứng minh tương tự ta có: CD là tia phân giác của góc C, BA là tia phân giác của góc B, DC là tia phân giác của góc D.
13 tháng 11 2016
a Đặt tên điểm nằm giữa là I nhé. Vì 2 đoạn thẳng AB và CD cắt nhau tại trung điểm nên suy ra 2 cạnh IC=ID Sau đó xét tam giác bằng nhau trường hợp cạnh-góc-cạnh và suy ra các đoạn thảng bằng nhau b Vì AB và CD vuông góc suy ra góc AID = 90 độ, xong tính các góc kia cũng ra 90 độ bằng cách 2 góc kề bù rồi chia 2 là ra tia p/g