Bài 4: (2 điểm) Cho góc nhọn xOy, kẻ tia phân giác Ot, lấy điểm M thuộc Ot. Kẻ MA vuông góc với Ox tại A, kẻ MB vuông góc với Oy tại B.. Chứng minh:
a) MA=MB và ![]()
b) Gọi D là điểm đối xứng của M qua Ox, E là điểm đối xứng của M qua Oy. Cmr: OD=OE

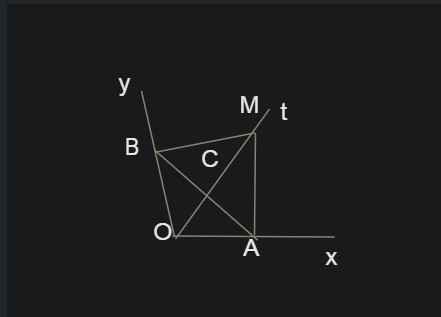
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB và OA=OB
b: M đối xứng D qua Ox
=>OM=OD
M đối xứng E qua Oy
=>OE=OM
=>OD=OE