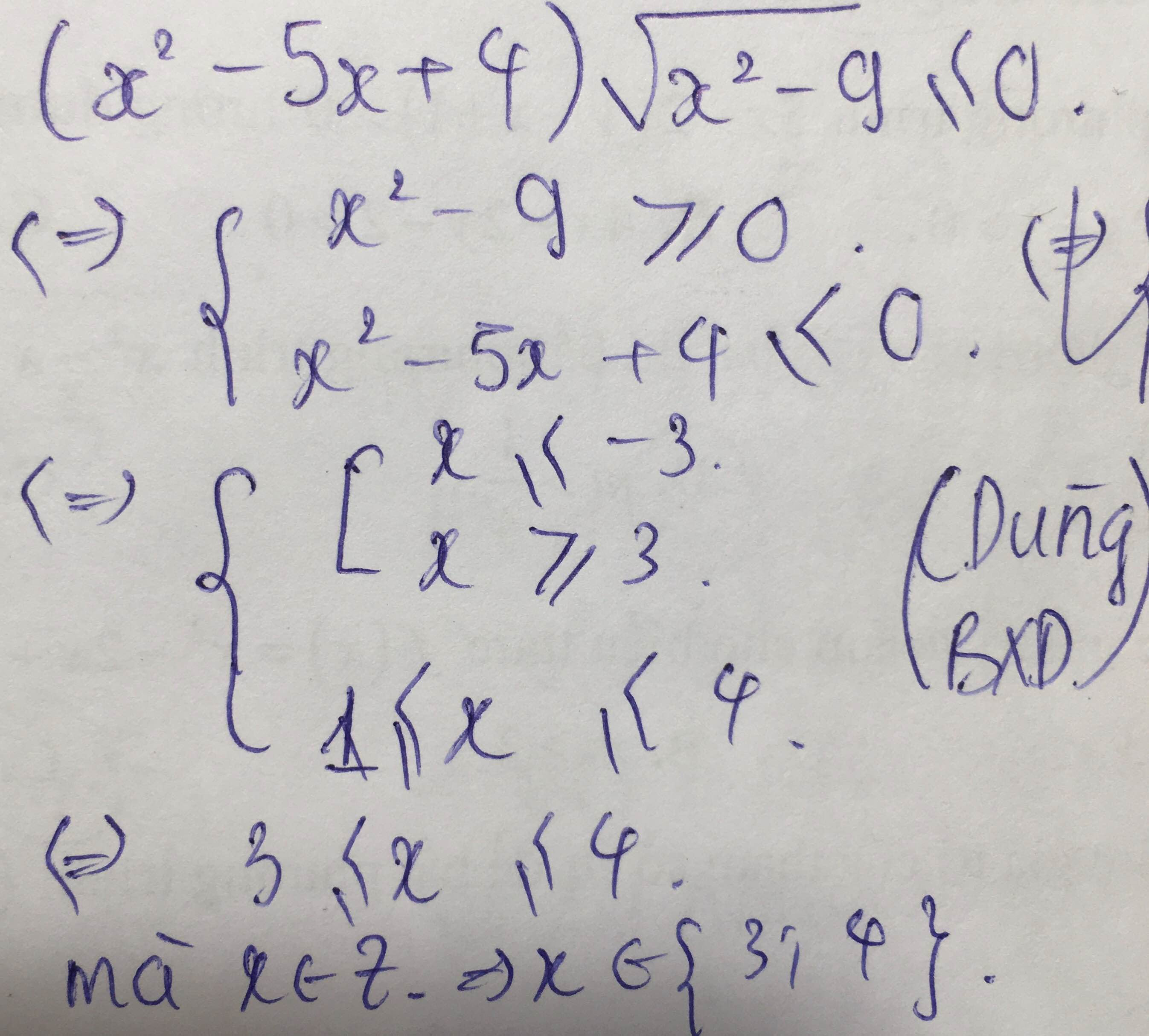
x=\(\left\{{}\begin{matrix}x=3\\x=-3\\x=-2\end{matrix}\right.\)

đề là \(\le\) 0 mà bạn 

\(x^2-5x+6\le0\Leftrightarrow\left(x-2\right)\left(x-3\right)\le0\Rightarrow2\le x\le3\) (1)

\(x^2-4\le0\Leftrightarrow\left(x-2\right)\left(x+2\right)\le0\Rightarrow-2\le x\le2\) (2)

(1);(2) \(\Rightarrow x=2\)

a/

\(\Leftrightarrow\frac{\left(x^2-1\right)\left(x^2+1\right)}{x^2+3x}+x^2-1\ge0\)

\(\Leftrightarrow\left(x^2-1\right)\left(\frac{x^2+1}{x^2+3x}+1\right)\ge0\)

\(\Leftrightarrow\left(x^2-1\right)\left(\frac{2x^2+3x+1}{x^2+3x}\right)\ge0\)

\(\Leftrightarrow\frac{\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(2x+1\right)}{x\left(x+3\right)}\ge0\)

\(\Leftrightarrow\frac{\left(x-1\right)\left(2x+1\right)\left(x+1\right)^2}{x\left(x+3\right)}\ge0\)

\(\Rightarrow\left[{}\begin{matrix}x< -3\\x=-1\\-\frac{1}{2}\le x< 0\\x\ge1\end{matrix}\right.\)

b/

\(\Leftrightarrow\left(x^2-1\right)\left(x^2-4\right)\left(\frac{-2-2x}{x}\right)\le0\)

\(\Leftrightarrow\frac{-2.\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+1\right)}{x}\le0\)

\(\Leftrightarrow\frac{\left(x+2\right)\left(x-1\right)\left(x-2\right)\left(x+1\right)^2}{x}\ge0\)

\(\Rightarrow\left[{}\begin{matrix}x\le-2\\x=-1\\0< x\le1\\x\ge2\end{matrix}\right.\)

c/

\(\Leftrightarrow\left(\frac{4\left(x-1\right)-2x}{x\left(x-1\right)}\right)\left(\frac{x^2+1-2x}{x}\right)\le0\)

\(\Leftrightarrow\frac{\left(2x-4\right)\left(x-1\right)^2}{x^2\left(x-1\right)}\le0\)

\(\Leftrightarrow\frac{\left(x-2\right)\left(x-1\right)^2}{x^2\left(x-1\right)}\le0\)

\(\Rightarrow1< x\le2\)

Tập nghiệm của BPT là: \(\left[{}\begin{matrix}-3< x\le-1\\0\le x< 1\\x>1\end{matrix}\right.\)

Câu 2,3,4 nx thôi ạ. Câu 1 có bạn giúp r ạ 

1)\(\sqrt{4x^2+12x+9}=2-x\)

\(\Leftrightarrow\sqrt{\left(2x+3\right)^2}=2-x\)

\(\Leftrightarrow\left|2x+3\right|=2-x\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+3=2-x\\2x+3=x-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-1\\x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-5\end{matrix}\right.\)

\(\)