Vận tốc của viên đạn súng trường m=10g khi ra khỏi nòng là 865m/s thời gian nó chuyển động trong nòng súng là 10-3s Tính động lượng của đoạn trích ra khỏi nòng súng độ biến thiên động lượng của Đảng trong thời gian đó thực thể trung bình của hơi thuốc lên đầu đạn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 2 2016
Giả sử thời gian đạn rời khỏi nòng súng là (rất nhỏ).
Giả sử nội lực của hệ đạn + nòng súng là N.
N làm biến thiên động lượng của đạn (đề đã bỏ qua tác động của trọng trường với đạn).
Hợp lực của N và F ma sát và P làm biến thiên động lượng của nòng.
Chiếu lên phương ngang.
Thay N từ pt trên vào ta tìm được V.
18 tháng 2 2022
Tham khảo:
m=80(g)=0,08(kg)
v0=0(m/s)
v=1000(m/s)
S=0,6(m)
Động năng của viên đạn khi bay ra khỏi nòng súng là:
Wđ=1/2mv2=1/2.0,08.10002
=40000(J)
Áp dụng định lí độ biến thiên động năng, ta có:
AF=1/2mv2−12mv20
⇔F.S=40000−0=40000
⇔F=40000/S=40000/0,6=2.105/3(N)
18 tháng 2 2022
Tham khảo:
\(m=80(g)=0,08(g)\)
\(v_0=0 (m/s)\)
\(v=1000(m/s)\)
\(S=0,6(m)\)
Động năng của viên đạn khi bay ra khỏi nòng súng là:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,08.1000^2=40000(J)\)
Áp dụng định lí độ biến thiên động năng, ta có:
\(A_F=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv^2_0\)
`<=>` \(F.S=40000-0=40000\)
`<=>` \(F=\dfrac{40000}{S}=\dfrac{4000}{0,6}=\dfrac{2.10^2}{3}(N)\)
6 tháng 3 2022
Biến thiên động lượng:
\(\Delta p=m\left(v_1-v_2\right)=0,025\cdot\left(800-0\right)=20kg.m\)/s
Mà \(\Delta p=F\cdot t\)
\(\Rightarrow F=\dfrac{\Delta p}{t}=\dfrac{20}{2,5}=8N\)
VT
9 tháng 5 2017
Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v → ⇒ V = − m M = − 3 m / s
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.
Chọn đáp án D
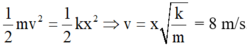
Động lượng viên đạn bay ra khỏi nòng:
\(p=m\cdot v=0,01\cdot865=8,65kg.m\)/s
Độ biến thiên động năng:
\(\Delta p=F\cdot\Delta t=0,01\cdot10\cdot10^{-3}=10^{-4}kg.m\)/s