Tóm tắt giúp mình luôn ạMột người dùng sợi dây kéo một chiếc hòm khối lượng 100 kg trên mặt sàn phẳng ngang để dời nó đi một đoạn 5 m. Biết hệ số ma sát là 0,2 và phương lực kéo hợp với mặt sàn góc 30°. Lấy g = 10 m/s2. Xác định công tối thiểu mà người này phải thực hiện để dịch chuyển chiếc...
Đọc tiếp
Tóm tắt giúp mình luôn ạ
Một người dùng sợi dây kéo một chiếc hòm khối lượng 100 kg trên mặt sàn phẳng ngang để dời nó đi một đoạn 5 m. Biết hệ số ma sát là 0,2 và phương lực kéo hợp với mặt sàn góc 30°. Lấy g = 10 m/s2. Xác định công tối thiểu mà người này phải thực hiện để dịch chuyển chiếc hòm.
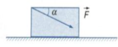
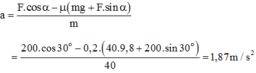
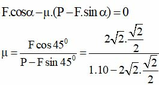
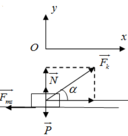
là 0,05. Lấy g = 10 m/s2 (hình 1).
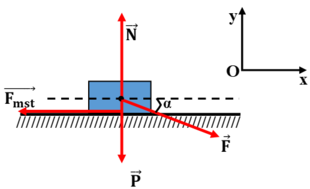
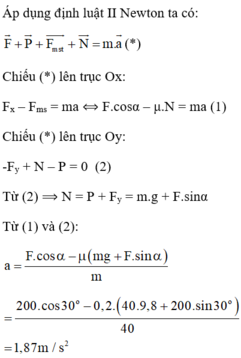
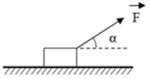
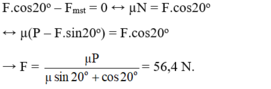
Tóm tắt: \(m=100kg;s=5m;\mu=0,2;\alpha=30^o\)
\(A=???\)
Lời giải:
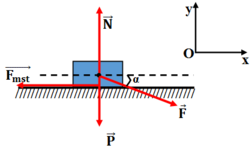
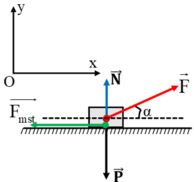
Theo quy tắc tổng hợp lực (quy tắc hình bình hành):
\(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
Em vẽ hình sẽ thấy: \(\left\{{}\begin{matrix}F_1=F\cdot cos\alpha\\F_2=F\cdot sin\alpha\end{matrix}\right.\)
Lực ma sát: \(F_{ms}=\mu\cdot N=\mu\cdot\left(P-F_2\right)=\mu\cdot\left(mg-F\cdot sin\alpha\right)\)
Dịch chuyển chiếc hòm, để thu được một công tối thiểu thì cần một lực nhỏ nhất.
\(\Rightarrow F_1=F_{ms}\Rightarrow F\cdot cos\alpha=\mu\cdot\left(mg-F\cdot sin\alpha\right)\)
\(\Rightarrow F\cdot cos30^o=0,2\cdot\left(100\cdot10-F\cdot sin30^o\right)\)
\(\Rightarrow F\approx207N\)
Công tối thiểu:
\(A=F_1\cdot s=F\cdot cos\alpha\cdot s=207\cdot cos30^o\cdot5=896,34J\)