Cho tam giác ABC nhọn nội tiếp đường tròn (O). Trên cung nhỏ AC lấy điểm D. Kẻ DE vuông góc với BC, DF vuông góc với ÁC
a) CMR: Tứ giác DFEC nội tiếp được đường tròn
b) Gọi G là giao điểm của AB và EF. CMR : Góc FED = Góc ABD và tam giác BDG vuông
c) Gọi I là trung điểm của EF, H là trung điểm của AB. CMR: Tam giác ABD đồng dạng với tam giác FED và IH vuông góc với DI

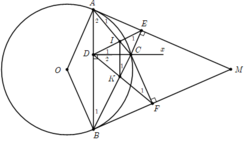
a) Xét tứ giác DFEC có
\(\widehat{DFC}=\widehat{DEC}\left(=90^0\right)\)
\(\widehat{DFC}\) và \(\widehat{DEC}\) là hai góc cùng nhìn cạnh DE
Do đó: DFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)