giải các pt sau bằng cách đặt ẩn phụ
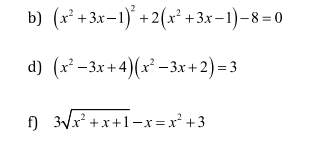
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\sqrt{x^2+x+1}=a\)
Pt trở thành \(3a=a^2+2\)
=>(a-1)(a-2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=1\\x^2+x+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+x=0\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{13}{4}\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{0;-1;\dfrac{\sqrt{13}-1}{2};\dfrac{-\sqrt{13}-1}{2}\right\}\)

\(5\sqrt{2x^3+16}=2\left(x^2+8\right)\left(x>-2\right)\)
\(\Leftrightarrow20\sqrt{\left(x+2\right)\left(x^2-2x+4\right)}=2\left(x^2+8\right)\)
\(\Leftrightarrow2\left(x^2+8\right)-20\sqrt{\left(x+2\right)\left(x^2-2x+4\right)}=0\)
\(\Leftrightarrow x^2+8-10\sqrt{x+2}\sqrt{x^2-2x+4}=0\)
\(\Leftrightarrow x^2-2x+4+2x+4-10\sqrt{x+2}\sqrt{x^2-2x+4}=0\)
Đặt a = \(\sqrt{x^2-2x+4}\left(a>0\right)\)
b = \(\sqrt{x+2}\left(b\ge0\right)\)
=> pt có dạng:
\(a^2-10ab+b^2=0\)
bạn phân tích rồi làm tiếp nhá

Đặt m = x - 1 .Điều kiện : m ≥ 0, x ≥ 1
Ta có : x - x - 1 -3 = 0 ⇔ (x -1) - x - 1 -2 =0
⇔ m 2 -m - 2 =0
Phương trình m 2 -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng
a – b + c = 0
Suy ra : m 1 = -1 (loại) , m 2 = -(-2)/1 = 2
Với m =2 ta có: x - 1 =2 ⇒ x -1 =4 ⇔ x =5
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=5

Đặt m = x/(x+1) .Điều kiện : x ≠ -1
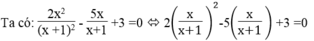
⇔ 2 m 2 -5m +3 =0
Phương trình 2m2 -5m +3 = 0 có hệ số a = 2, b = -5 , c = 3 nên có dạng
a +b + c = 0
suy ra : m 1 = 1 , m 2 =3/2
Với m 1 =1 ta có: x/(x+1) =1 ⇔ x =x+1 ⇔ 0x =1 (vô nghiệm)
Với m = 3/2 ta có: x/(x+1) = 3/2 ⇔ 2x =3(x +1)
⇔ 2x =3x +3 ⇔ x =-3
Giá trị của x thỏa mãn điều kiện bài toán
Vậy phương trình đã cho có 1 nghiệm : x=-3

ĐKXĐ : \(1\le x\le3\)
\(x-\sqrt{x-1}-3=0\)
\(\Leftrightarrow\left(x-1\right)-\sqrt{x-1}-2=0\)
Đặt \(t=\sqrt{x-1},t\ge0\), suy ra pt trên trở thành \(t^2-t-2=0\Leftrightarrow\left(t-2\right)\left(t+1\right)=0\Leftrightarrow\orbr{\begin{cases}t=2\left(\text{nhận}\right)\\t=-1\left(\text{loại}\right)\end{cases}}\)
Với t = 2 suy ra x = 5

Đặt m= x 2 -3x +2
Ta có: ( x 2 -3x +4)( x 2 -3x +2) =3
⇔ [( x 2 -3x +2 +2)( x 2 -3x +2) -3 =0
⇔ x 2 - 3 x + 2 2 +2( x 2 -3x +2) -3 =0
⇔ m 2 +2m -3 =0
Phương trình m 2 +2m -3 = 0 có hệ số a = 1, b = 2 , c = -3 nên có dạng
a +b+c=0
suy ra : m 1 =1 , m 2 =-3
Với m 1 =1 ta có: x 2 -3x +2 =1 ⇔ x 2 -3x +1=0
∆ = - 3 2 -4.1.1 = 9 -4 =5 > 0
∆ = 5
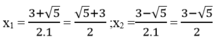
Với m 2 =-3 ta có: x 2 -3x +2 =-3 ⇔ x 2 -3x +5=0
∆ = - 3 2 -4.1.5 = 9 -20 =-11 < 0.Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
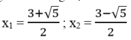

Đặt m =4x -5
Ta có: 4 x - 5 2 – 6(4x -5) +8 =0 ⇔ m 2 -6m +8 =0
∆ ’ = - 3 2 -1.8 =9 -8=1 > 0
∆ ' = 1 = 1
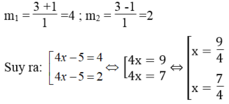
Vậy phương trình đã cho có 2 nghiệm x 1 =9/4 , x 2 =7/4
b: \(\Leftrightarrow\left(x^2+3x-1\right)^2+4\left(x^2+3x-1\right)-2\left(x^2+3x-1\right)-8=0\)
\(\Leftrightarrow\left(x^2+3x-1\right)\left(x^2+3x-1+4\right)-2\left(x^2+3x-1+4\right)=0\)
\(\Leftrightarrow x^2+3x-3=0\)
\(\Delta=3^2-4\cdot1\cdot\left(-3\right)=9+12=21>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{21}}{2}\\x_2=\dfrac{-3+\sqrt{21}}{2}\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x^2-3x\right)^2+6\left(x^2-3x\right)+8=3\)
\(\Leftrightarrow\left(x^2-3x\right)^2+5\left(x^2-3x\right)+\left(x^2-3x\right)+5=0\)
\(\Leftrightarrow x^2-3x+1=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{5}}{2}\\x_2=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)