đây là bài lớp 7 mà tớ có lớp 6 nên mún hỏi tham khảo í mà

a: Xét ΔABD và ΔACD có

AB=AC

AD chung

BD=CD

Do đó: ΔABD=ΔACD

a) Ta chứng minh:

S A E F = S A B C D = 1 4 S A B F  

b) Từ câu a suy ra EH = CK

c) Gọi S_BDE = S₁; S_ADE = S₂;

Ta chứng minh DE = DC;

Ta tính được:

A_BDC = S₁; S_ADC = S₂, suy ra S_ABC = 2(S₁ + S₂) = 2.S_ABD

a: Xét ΔEBC và ΔFCB có

EB=FC

góc EBC=góc FCB

BC chung

=>ΔEBC=ΔFCB

=>EC=FB

b: Xét ΔIBC có góc IBC=góc ICB

nên ΔICB cân tại I

=>IB=IC

Xét ΔIBE và ΔICF có

IB=IC

IE=IF

BE=CF
=>ΔIBE=ΔICF

c: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC
=>ΔAIB=ΔAIC

=>góc IAB=góc IAC

=>AI là phân giáccủa góc BAC

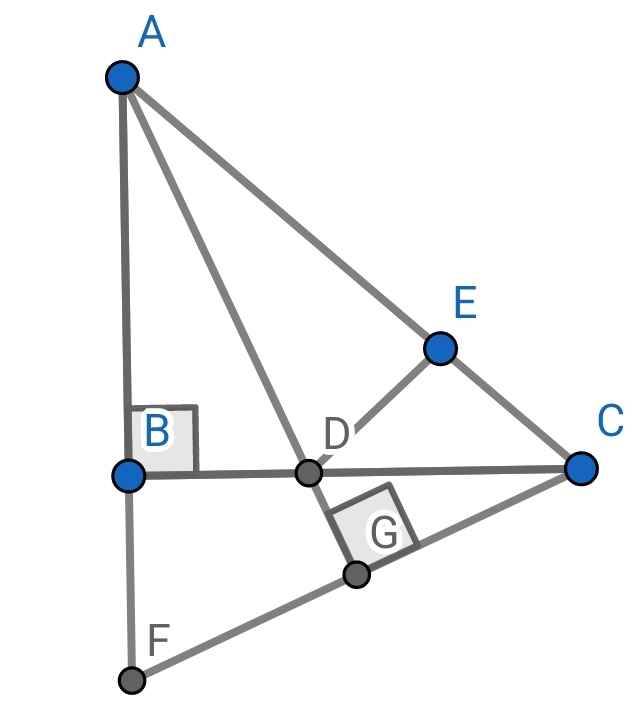
a) Xét ∆ADB và ∆ADE có:

AD chung

Góc BAD = góc EAD (AD là tia phân giác của góc BAC)

AB = AE (gt)

⇒∆ADB = ∆ADE (c-g-c)

b) Do ∆ADB = ∆ADE (c-g-c)

⇒góc ABD = góc AED (hai góc tương ứng)

⇒góc AED = 90⁰

Hay DE vuông góc AC

c) Gọi G là giao điểm của CF và AD

Do góc BAD = góc EAD (cmt)

⇒góc FAG = góc CAG

Xét hai tam giác vuông: ∆AGF và ∆AGC có:

AG chung

góc FAG = góc CAG (cmt)

⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)

⇒AF = AC (hai cạnh tương ứng)

Mà AF = AB + BF

AC = AE + EC

AB = AE

⇒BF = CE

a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có

BC chung

\(\widehat{FBC}=\widehat{ECB}\)

DO đó: ΔFBC=ΔECB

Suy ra: FB=EC

b: Ta có: AF+FB=AB

AE+EC=AC

mà BF=CE

và AB=AC

nên AF=AE

Xét ΔABC có AF/AB=AE/AC

nên FE//BC

Ta có : AB = AE + BF
AC = AF + CF
mà AE = AF( gt) , AB = AC ( gt)
=> BE = CF
Vì Δ ABC có AB = AC ( gt)
=> Δ ABC là tam giác cân
=> góc B = C
Xét ΔBEC và ΔCFB có :
góc B = C ( cmt )
BE = CF ( cmt )
BC là cạnh chung ( gt)
=> ΔBEC = ΔCFB ( c- g-c )( đcpcm)

1:

Sửa đề: ΔBEC

Xét ΔHBC vuông tại H và ΔBEC vuông tại B có

góc HCB chung

=>ΔHBC đồng dạng với ΔBEC

2: ΔHBC đồng dạng với ΔBEC

=>CH/CB=BH/BE

=>CH/CD=BH/BF

ko đc sửa đề bạn ơi