Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc vói BC tại H. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.
a) Chứng minh AH2 - AE.AB.
b) Chứng minh Δ A F E ~ Δ A B C ;
c) Lấy M đối xứng với A qua E, tia MH cắt cạnh AC tại N. Chứng minh A B H ^ = A N H ^ và EF//HN.
d) Gọi O là trung điểm của BC; AO giao với HN tại K. Cho biết A C B ^ = 30 ° , hãy tính tỉ số A K A N S H C A

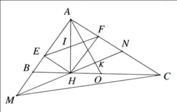
a: ΔAHB vuông tại H có HE là đường cao
nên AH^2=AE*AB
b: ΔAHC vuông tại H có HF là đường cao
nên AH^2=AF*AC
=>AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB