A = xyz ( 2x + 4y - 5x + y - 1)

= xyz ( 5y - 3x - 1 )

A. KQ là -1

B. KQ là 21

C. KQ là 6,75

tick mik nha

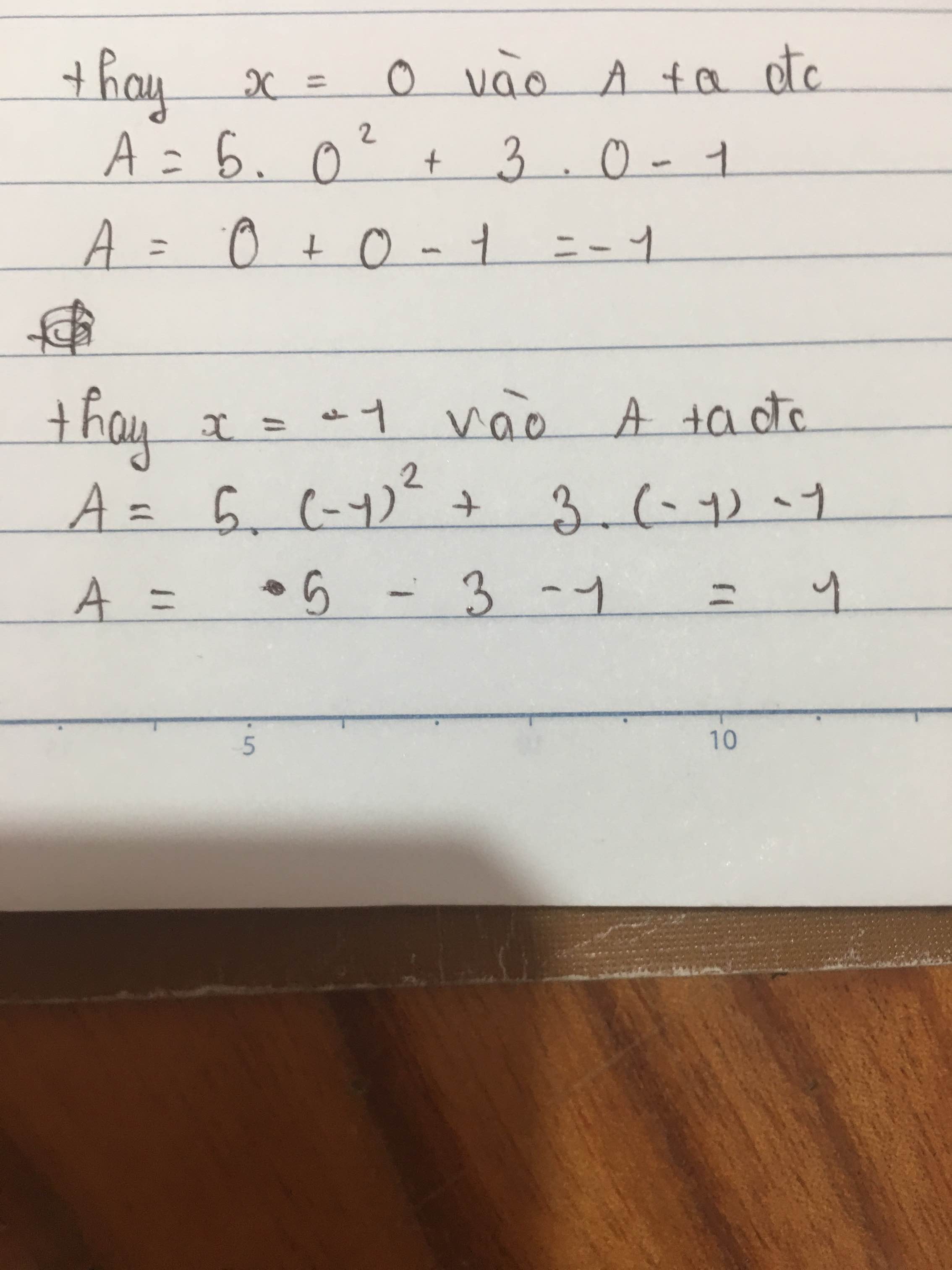
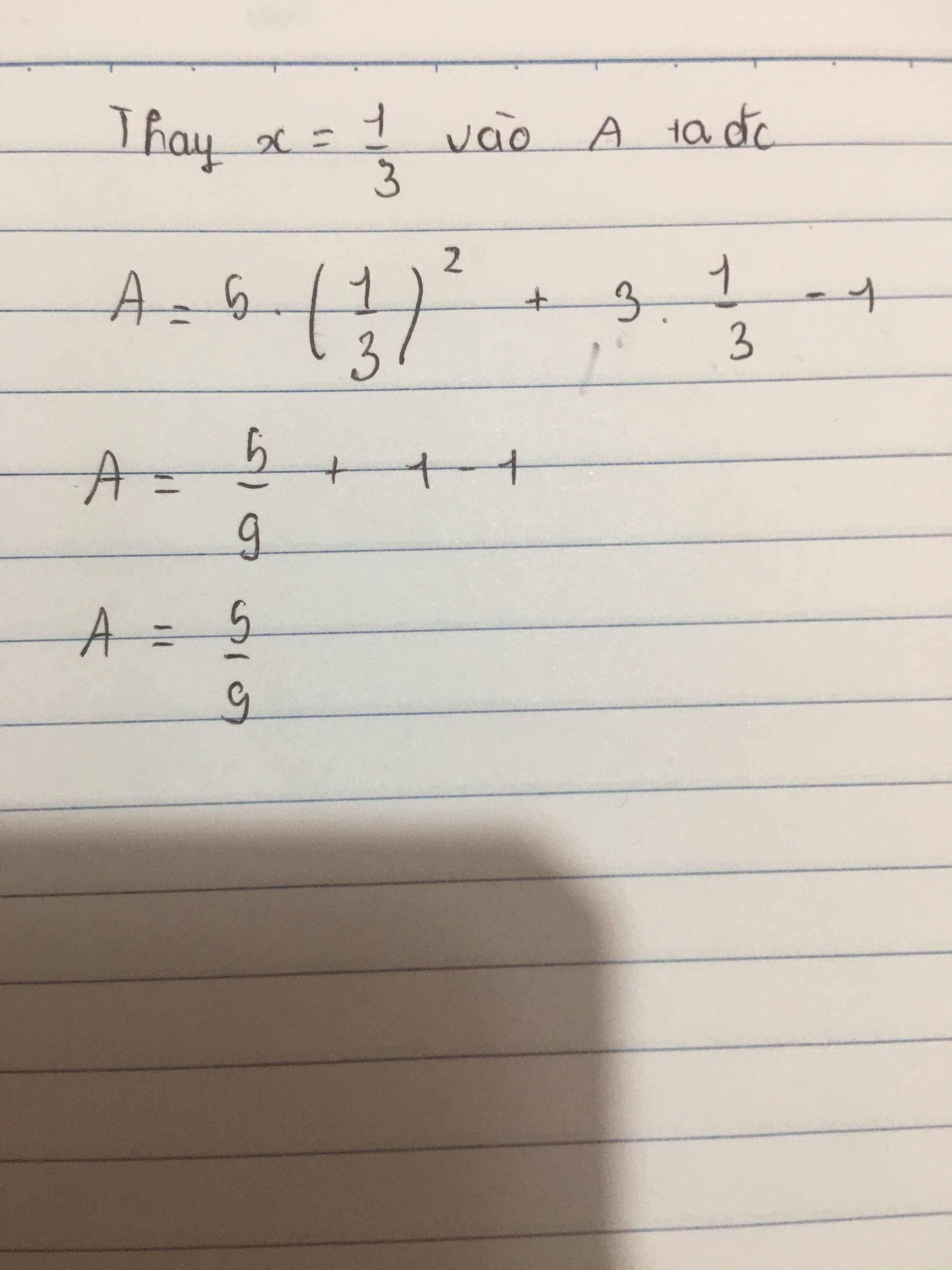
e:

Xét ΔABH và ΔACH có

AB=AC
góc BAH=góc CAH

AH chung

=>ΔABH=ΔACH

Xét ΔABC có

AH,BM là trung tuyến

AH cắt BM tại G

=>G là trọng tâm

BH=CH=9cm

=>AH=căn 15^2-9^2=12cm

Xét ΔABC có

H là trung điểm của BC

HK//AC

=>K là trug điểm của AB

=>C,G,K thẳng hàng

d: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có

OM chung

góc AOM=góc BOM

=>ΔOAM=ΔOBM

=>MA=MB

Xét ΔMAH vuông tại A và ΔMBK vuông tại B có

MA=MB

góc AMH=góc BMK

=>ΔMAH=ΔMBK

OA+AH=OH

OB+BK=OK

mà OA=OB và AH=BK

nên OH=OK

=>ΔOHK cân tại O

mà OI là phân giác

nên OI vuông góc HK

b: A(x)=0

=>x-7=0

=>x=7

Bài 1:

$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$ 

$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$

$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$

Bài 2:
$8x^3-32y-32x^2y+8x=0$

$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$

$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$

$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)

$\Leftrightarrow x=4y$

Khi đó:

$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

1, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-6\end{matrix}\right.\)

\(A=\left(x_1-2x_2\right)\left(2x_1-x_2\right)\\ =2x_1^2-4x_1x_2-x_1x_2+2x_1^2\\ =2\left(x_1^2+x_2^2\right)-5x_1x_2\\ =2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\\ =2\left(-5\right)^2-4.\left(-6\right)-5.\left(-6\right)\\ =104\)

2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=-3\end{matrix}\right.\)

\(B=x_1^3x_2+x_1x_2^3\\ =x_1x_2\left(x_1^2+x_2^2\right)\\ =\left(-3\right)\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\left(-3\right)\left[5^2-2\left(-3\right)\right]\\ =-93\)

chịu

a) Ta có: \(B=\dfrac{x^2}{5x+25}+\dfrac{2\left(x+5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\)

\(=\dfrac{x^2}{5\left(x+5\right)}+\dfrac{2\left(x+5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\)

\(=\dfrac{x^3}{5x\left(x+5\right)}+\dfrac{10\left(x+5\right)^2}{5x\left(x+5\right)}+\dfrac{250+25x}{5x\left(x+5\right)}\)

\(=\dfrac{x^3+10x^2+100x+250+250+25x}{5x\left(x+5\right)}\)

\(=\dfrac{x^3+10x^2+125x+500}{5x\left(x+5\right)}\)

\(=\dfrac{x^3+5x^2+5x^2+25x+100x+500}{5x\left(x+5\right)}\)

\(=\dfrac{x^2\left(x+5\right)+5x\left(x+5\right)+100\left(x+5\right)}{5x\left(x+5\right)}\)

\(=\dfrac{\left(x+5\right)\left(x^2+5x+100\right)}{5x\left(x+5\right)}\)

\(=\dfrac{x^2+5x+100}{5x}\)

b) Thay x=-2 vào biểu thức \(B=\dfrac{x^2+5x+100}{5x}\), ta được:

\(B=\dfrac{\left(-2\right)^2+5\cdot\left(-2\right)+100}{-5\cdot2}=\dfrac{4+100-10}{-10}=\dfrac{94}{-10}=-\dfrac{94}{10}=\dfrac{-47}{5}\)

Vậy: Khi x=-2 thì \(B=-\dfrac{47}{5}\)

\(a,ĐK:x\ne-3;x\ne0;y\ne0\\ b,A=\dfrac{1}{x^2\left(x+3\right)+y^2\left(x+3\right)}=\dfrac{1}{\left(x^2+y^2\right)\left(x+3\right)}\\ x=y=0\Leftrightarrow A\in\varnothing\)